ローレンツ力
ローレンツ力とは、電磁場の中で運動する荷電粒子が受ける力です。ローレンツ力 $F$ と電場 $E$ 、磁束密度 $B$ 、電荷 $q$ 、荷電粒子の速度 $v$ の関係は以下で表されます。
$${\bf F}=q{\bf E}+q{\bf v}\times{\bf B}$$
特に右辺第1項はクーロン力と呼ばれており、第2項は狭義のローレンツ力になります。以下は、この狭義のローレンツ力の特徴について述べます。
右ネジの法則
右ネジの法則とは、ドライバを回す方向とネジが進む方向の関係です。ローレンツ力は速度と電束密度がベクトル積になっているため、速度を磁束密度に重ねる方向(黄色の矢印)をドライバを回す方向と考えた場合、ローレンツ力の働く方向は右ネジの進む方向に相当します。
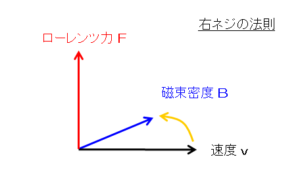
尚、速度を ${\bf v}=(v,0,0)$、磁束密度を ${\bf B}=(0,B,0)$ とした場合、ローレンツ力は $(0,0,qvB)$ となります。尚、負の電荷をもつ荷電粒子の場合は、ローレンツ力の方向は正の電荷の逆になります。
エネルギーの保存
ローレンツ力は荷電粒子に対して仕事をしません。これは次のようにして確認できます。
$$\Delta W={\bf F}\cdot\Delta{\bf r}=(q{\bf v}\times{\bf B})\cdot{\bf v}\Delta t=0$$
つまり、ローレンツ力による運動エネルギーの変化はなく、荷電粒子の速度も変わりません。
サイクロトロン運動
サイクロトロン運動とは、磁場中の荷電粒子が描く回転運動です。この回転運動の半径はラーモア半径と呼ばれ、ローレンツ力と荷電粒子にかかる遠心力の釣り合う距離として定まります。磁場に垂直な面上の速度を $v_\perp$ とすると、
$$|q|v_\perp B=\frac{mv_\perp^2}{r}$$
従って、ラーモア半径は以下で表されます。
$$r_L=\frac{mv_\perp}{|q|B}$$
また、回転の振動数(サイクロトロン周波数)は以下になります。
$$\omega_c=\frac{2\pi}{T_c}=\frac{|q|B}{m}$$$$T_c=\frac{2\pi r_L}{v_\perp}$$
フレミング左手の法則
フレミング左手の法則とは、電流の方向に対する導体に働く力(ローレンツ力)の方向を示す法則で、電流の方向を左手の中指、磁場の方向を同じく人差し指とすると、導体に働く力(ローレンツ力)は親指の方向になります。
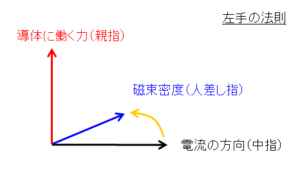
これは先の右ネジの法則の別の表現となります。
フレミング右手の法則
フレミングの右手の法則は、磁場内を運動する導体内に発生する起電力(電流)の方向を示す法則で、導体の動いた方向を右手の親指、磁場の方向を人差し指とすると、起電力は中指の方向になります。
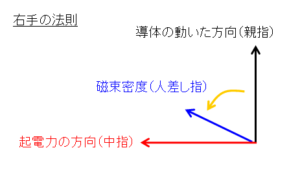
これも右ネジの法則の別の表現に過ぎず、導体の動いた方向(荷電粒子の速度の方向)を磁場に重ねる方向(黄色の矢印)に対する右ネジの進む方向が、起電力(ローレンツ力)の働く方向に相当します。




