コリオリの力とは
コリオリの力とは、慣性系に対して回転する座標系内を運動する物体に作用する慣性力または見かけの力です。左回り(反時計回り)に回転する座標系では、この力は物体の進行方向の右側に働き、右回り(時計回り)では力は左側に働きます。
静止座標系を ${\bf R}=(X,Y,Z)$ 、回転座標系を ${\bf r}=(x,y,z)$ 、角速度ベクトルを ${\bf\omega}=(0,0,\omega)$ とすると、回転座標系上を運動する質点 $m$ の運動方程式は以下のように書くことができます(導出)。
$$m\ddot{x}=F_x+2m\omega\dot{y}+m\omega^2x+m\dot{\omega}y -①$$$$m\ddot{y}=F_y-2m\omega\dot{x}+m\omega^2y-m\dot{\omega}x -②$$$$m\ddot{z}=F_z$$
これをベクトルで書くと以下になります。
$$m\ddot{\bf r}={\bf F}-2m{\bf\omega}\times\dot{\bf r}+m\omega^2{\bf r}-m\dot{\bf\omega}\times{\bf r}$$
右辺第1項の質点に働く外力 ${\bf F}$ の他、3種類の回転による見かけの力が働きます。
- 右辺第2項:$-2m{\bf\omega}\times\dot{\bf r}$
⇒コリオリの力 - 右辺第3項:$m\omega^2{\bf r}$
⇒遠心力 - 右辺第4項:$-m\dot{\bf\omega}\times{\bf r}$
⇒角速度が一定($\dot{\omega}=0$)の場合が現れない
下図のように左回り(反時計回り)の回転系の場合、角速度ベクトル ${\bf \omega}$ は、画面の裏面から表面を向いています。この回転系の上を速度 ${\bf v}$ で運動する質点を考えると、コリオリの力は常に質点の進行方向の右側($-{\bf\omega}\times{\bf v}$)に働きます。
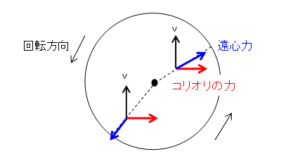
地球の北半球を北極側から見下ろすと、地球は上図と同様、左回り(西から東)に回転しています。このため、台風の目に吹き込む風には右向きの力が働き、台風の風は左回り(反時計回り)に回転します。従って、台風の風は、台風の目の東側で強くなる傾向があります。
一方、南半球を南極側から見下ろすと、地球は上図の逆の右回り(西から東)に回転しています。このため、台風の目に吹き込む風には左向きの力が働き、台風の風は右回り(時計回り)に回転します。
コリオリの力の導出
①②を導く
静止座標系 ${\bf R}=(X,Y,Z)$ に対する回転座標系 ${\bf r}=(x,y,z)$ の角度を $\theta$ とします。
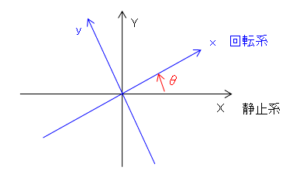
この場合、両座標系間の変換は以下で表されます。
$$X=x\cos{\theta}-y\sin{\theta}$$$$Y=x\sin{\theta}+y\cos{\theta}$$
時間微分を行うと、
$$\dot{X}=\dot{x}\cos{\theta}-x\dot{\theta}\sin{\theta}-\dot{y}\sin{\theta}-y\dot{\theta}\cos{\theta}$$$$\dot{Y}=\dot{x}\sin{\theta}+x\dot{\theta}\cos{\theta}+\dot{y}\cos{\theta}-y\dot{\theta}\sin{\theta}$$
もう1回時間微分を行うと、
$\ddot{X}=(\ddot{x}-2\dot{y}\dot{\theta}-x\dot{\theta}^2-y\ddot{\theta})\cos{\theta}$
$-(\ddot{y}+2\dot{x}\dot{\theta}-y\dot{\theta}^2+x\ddot{\theta})\sin{\theta} -(1)$
$\ddot{Y}=(\ddot{x}-2\dot{y}\dot{\theta}-x\dot{\theta}^2-y\ddot{\theta})\sin{\theta}$
$+(\ddot{y}+2\dot{x}\dot{\theta}-y\dot{\theta}^2+x\ddot{\theta})\cos{\theta} -(2)$
一方、加速度についても同様に座標変換されるため、
$$A_X=a_x\cos{\theta}-a_y\sin{\theta} -(3)$$$$A_Y=a_x\sin{\theta}+a_y\cos{\theta} -(4)$$
(1) 、(2) と (3) 、(4) を見比べると、
$$a_x=\ddot{x}-2\dot{\theta}\dot{y}-\dot{\theta}^2x-\ddot{\theta}y$$$$a_y=\ddot{y}+2\dot{\theta}\dot{x}-\dot{\theta}^2y+\ddot{\theta}x$$
運動方程式 ${\bf F}=m{\bf a}$ より、
$$m\ddot{x}=F_x+2m\dot{\theta}\dot{y}+m\dot{\theta}^2x+m\ddot{\theta}y$$$$m\ddot{y}=F_y-2m\dot{\theta}\dot{x}+m\dot{\theta}^2y-m\ddot{\theta}x$$
ここで、$\theta=\omega t$ 、$\dot{\theta}=\omega$ 、$\ddot{\theta}=\dot{\omega}$ と置くと、
$$m\ddot{x}=F_x+2m\omega\dot{y}+m\omega^2x+m\dot{\omega}y \to①$$$$m\ddot{y}=F_y-2m\omega\dot{x}+m\omega^2y-m\dot{\omega}x \to②$$
これにより①と②が得られることが分かります。




