ケプラーの法則とは
ケプラーの法則とは、17世紀初頭に天文学者のケプラーにより発見された、惑星の運動に関する法則です。ケプラーは、天文学者のブラーエの膨大な観測記録から、太陽に対する火星の運動を推定し、３つの法則としてまとめました。
- 第１法則：楕円の法則
- 第２法則：面積速度一定の法則
- 第３法則：周期と長径の法則
そして、これらのケプラーの法則は、ニュートンの運動方程式から導くことができます。
運動方程式を解く
ここでは、惑星の運動方程式を導きます。まず、中心力でのニュートンの運動方程式（$r$ 成分）は以下になります。
$$F_r=mA_r=m(\ddot{r}-r\dot{\theta}^2)$$
恒星と惑星の万有引力を以下で表されます。
$$F_r=-\frac{GmM}{r^2}$$
これを $r$ 方向の運動方程式に代入すると以下になります。ここで、$l=mr^2\dot{\theta}$ で角運動量を表します。
$$\frac{d^2r}{dt^2}+\frac{GM}{r^2}-\frac{l^2}{m^2r^3}=0 －①$$
運動方程式を解くと以下の解が得られます。この式の導出はこの記事の最後で行います。
$$r=\frac{\lambda}{1+\epsilon\cos{\theta}} －②$$
$$\lambda\equiv\frac{l^2}{GMm^2} , \epsilon\equiv\frac{Cl^2}{GMm^2}$$
②を導く
①から②の導出を行います。まず、①で時間微分を $\theta$ の微分に置換えます。$\dot{\theta}=l/mr^2$ であることから、
$$\frac{d}{dt}=\frac{d\theta}{dt}\frac{d}{d\theta}=\frac{l}{mr^2}\frac{d}{d\theta}$$
であるため、以下のように置き換えられます。
$$\frac{d^2r}{dt^2}=\frac{l^2}{m^2r^2}\frac{d}{d\theta}\left(\frac{1}{r^2}\frac{dr}{d\theta}\right)$$
次に $u=1/r$ と置くと、
$$\frac{1}{r^2}\frac{dr}{d\theta}=-\frac{du}{d\theta}$$
となるため、以下のように書き換えられます。
$$\frac{d^2r}{dt^2}=-\frac{l^2u^2}{m^2}\frac{d^2u}{d\theta^2}$$
これを①に代入すると、以下になります。
$$\frac{d^2u}{d\theta^2}=-u+\frac{GMm^2}{l^2}$$
この微分方程式の解が以下であることは、実際に代入してみると分かります。ここで $C$ と $\alpha$ は積分定数です。
$$u=C\cos{(\theta+\alpha)}+\frac{GMm^2}{l^2}$$
最後に、$r=1/u$、$\alpha=0$ とすると②になります。
ケプラーの法則を説明する
第１法則：楕円の法則
第１法則とは、惑星は恒星の周りを楕円軌道を描いて公転し、恒星は楕円の焦点に１つに位置することです。
惑星の運動方程式を解いて得られる以下の式は、惑星の軌道が楕円であることを表しています。
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 －③$$
$$a\equiv\frac{\lambda}{1-\epsilon^2} , b\equiv\frac{\lambda}{\sqrt{1-\epsilon^2}}$$
③を導く
②の式は楕円を描きますが、これは以下のように示せます。
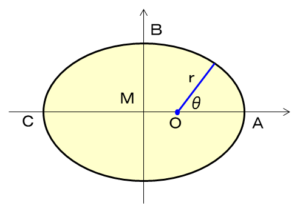
$\theta=0$ を横軸方向にとると、
$$\overline{OA}=r(\theta=0)=\frac{\lambda}{1+\epsilon}$$
$$\overline{OC}=r(\theta=\pi)=\frac{\lambda}{1-\epsilon}$$
であるから、長径 $a$ は、
$$a\equiv\overline{MA}=\frac{\overline{OA}+\overline{OC}}{2}=\frac{\lambda}{1-\epsilon^2}$$
また、$\theta$ が $B$ まで来たとき、
$$\overline{OM}=-r\cos{\theta} (\theta\gt\pi/2)$$
$$\overline{OM}=a-\overline{OA}=\frac{\lambda\epsilon}{1-\epsilon^2}$$
となるため、ここで得られた $\cos{\theta}$ を②に代入すると、
$$\overline{OB}=r=\frac{\lambda}{1-\epsilon^2}$$
であるから、短径 $b$ は、
$$b\equiv\overline{MB}=\sqrt{\overline{OB}^2-\overline{OM}^2}=\frac{\lambda}{\sqrt{1-\epsilon^2}}$$
さらに、$M$ を中心とした $x,y$ 座標で表すと、
$$x=\overline{OM}+r\cos{\theta}=\frac{\lambda\epsilon}{1-\epsilon^2}+\frac{\lambda\cos{\theta}}{1+\epsilon\cos{\theta}}$$
$$y=r\sin{\theta}=\frac{\lambda\sin{\theta}}{1+\epsilon\cos{\theta}}$$
これらより、③が成り立つことを確認することができます。
第２法則：面積速度一定の法則
第２法則とは、面積速度$\Delta$が一定となることで、角運動量の保存により導くことが得きます。 ここで $\phi$ は速度 $V$ の $r$ 方向とのなす角度です。
$$\Delta=\frac{1}{2}rV_\theta=\frac{1}{2}rV\sin{\phi}=\frac{l}{2m}$$
第３法則：周期と長径の法則
第３法則は、公転周期の２乗は長半径の３乗に比例するという法則です。公転周期は楕円の面積 $S$ を面積速度で割ると得られる。
$$T=\frac{S}{\Delta}=\frac{\pi ab}{\Delta}=\frac{2\pi m\lambda^2}{l(1-\epsilon^2)^{3/2}}$$
$$T^2=\frac{4\pi^2}{GM}a^3$$
