巡回冗長検査（CRC）とは

巡回冗長検査
CRCの計算

巡回冗長検査

巡回冗長検査（Cyclic Redundancy Check；以下、CRC ）とは、巡回符号の理論に基づいた誤り検出符号の一種で、主にデータ転送などに伴う偶発的な誤りの検出に使われています。

送信側は定められた生成多項式（除数）で除算した余り（剰余）を検査データとして付加して送信し、受信側で同じ生成多項式を使用してデータを除算し、その余りを比較することによって受信データの誤りを検出することができます。

CRC にはいくつかの種類があり、出力結果（剰余）のビット幅や生成多項式によって分けられます。出力結果が n ビットになる場合は、「CRC-n」と表記され、規格によって生成多項式が異なる場合は、「CRC-n XXX」のように表記されます。

主な生成多項式には以下のものがあります。「CRC-n」の場合はｎ次の生成多項式が使用されます。

CRC-4-ITU	$x^4+x+1$
CRC-8	$x^8+x^7+x^6+x^4+x^2+1$
CRC-16	$x^{16 }+x^{15}+x^2+1$
CRC-32	$x^{32}+x^{26}+x^{23}+x^{22}+x^{16}+x^{12}+x^{11}+x^{10}$ $+x^8+x^7+x^5+x^4+x^2+x+1$

CRCの計算

送信するデータを10進法で $4321$（２進法：$0001\,0000\,1110\,0001$ ；以下、被除数）、生成多項式を CRC-4-ITU（ $x^4+x+1$ ）として、CRC の値（以下、剰余）を求める手順を示します。生成多項式をビットで表すと、$10011$（以下、除数）となります。

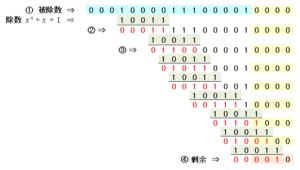
被除数の右に４ビットの剰余ビット $0000$ を追加します。４次の生成多項式を利用しているため、剰余ビットも４ビットとなります。（①）
除数の左端の $1$ を被除数の最初に表れる $1$ に合わせて、排他論理和（以下、XOR）を取ります。XOR を取っていない被除数と剰余ビットはそのまま下します。尚、XOR の入力と出力の関係は以下になります。（②）

入力 $0$ $0$ $1$ $1$

$0$ $1$ $0$ $1$

出力 $0$ $1$ $1$ $0$
同様に、除数の左端の $1$ を②の最初に表れる $1$ に合わせて、XOR を取ります。XOR を取っていない被除数と剰余ビットはそのまま下します。（③）
これを繰り返し、最後に残った４ビットの値が求める剰余（ CRC の値）です。（④）
この CRC 値を送信データに付けて送信します。