ファラデーの電磁誘導の法則
ファラデーの電磁誘導の法則とは、閉回路に生じる誘導起電力の大きさは、その回路を貫く磁場の変化の割合に比例するという法則です。19世紀前半にファラデーによって発見されました。
任意の閉回路内の領域 $S$ を通る磁束の変化と、閉回路に沿って発生する電場は比例関係にあります。これを式で表すと以下になります。右辺のマイナスは、磁束 $\Phi$ の変化を打ち消す方向に誘導起電力(電場 $E$)が発生することを示します。
$$\oint_S{\bf E}\cdot d{\bf s}=-\frac{d\Phi}{dt}$$
これをストークスの定理を用いて左辺を面積分に書き直し、右辺を磁束密度 $B$ を使って書き直すと、
$$\int_S\nabla\times{\bf E}\cdot d{\bf S}=-\frac{d}{dt}\int_S{\bf B}\cdot d{\bf S}$$
となるため、以下の式が得られます。
$$\nabla\times{\bf E}=-\frac{d{\bf B}}{dt}$$
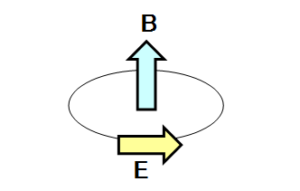
これが、微分形式で表されたファラデーの電磁誘導の法則で、マクスウェル方程式の1つに含まれています。尚、電場 $E$ と電束密度 $B$ の向きは右ネジの関係になります。
レンツの法則
レンツの法則とは、磁束の変化によってコイルに発生する起電力は、コイルを貫く磁束の変化に比例し、発生する誘導電流の向きは磁束の変化を妨げるような向きになるとする法則です。19世紀前半にレンツにより発見されました。
コイルを貫く磁束に変化 $\Delta\Phi$ があったときのコイルの誘導起電力 $V$ は、コイルの巻き数を $N$ とすると以下で表されます。これは、コイルの巻き数に比例して起電力も大きくなることが分かります。
$$V=-N\frac{\Delta\Phi}{\Delta t}$$
これは、先に紹介したファラデーの電磁誘導の法則と同じことを表しています。
単位まとめ
| 名称 | 記号 | 単位 | 次元 |
| 電圧 | $V$ | $V$(ボルト) | $ML^2T^{-3}I^{-1}$ |
| 磁束 | $\Phi$ | $Wb$(ウェーバ) | $ML^2T^{-2}I^{-1}$ |
| 電場の強さ | $E$ | $V/m$ | $MLT^{-3}I^{-1}$ |
| 磁場の強さ | $H$ | $A/m$ | $L^{-1}I$ |
| 電束密度 | $D$ | $C/m^2$ | $L^{-2}TI$ |
| 磁束密度 | $B$ | $T$(テスラ) | $MT^{-2}I^{-1}$ |





