量子もつれ(entanglement)とは、古典物理学では説明できない、複数の粒子間の相関現象です。本記事では、光子の偏光を例にとり、量子もつれを説明します。
光子の偏光
古典的な光は波として表され、その振幅の方向は、光波の進行方向に対し垂直(垂直面上)になります。通常は、その垂直面上の振幅方向に偏りはありませんが、偏光板を通過すると、1つの方向に揃った状態(偏光)になります。このとき、偏光板を通過した光の強さは半分になります。
x軸方向に偏光させる偏光板(以下、偏光板X)を2枚重ねた場合、1枚目の偏光板Xを通過した光は、全て2枚目の偏光板Xも通過します。2枚目の偏光板がy軸方向に変更させる偏光板(以下、偏光板Y)の場合は、1枚目を通過した光は、全て2枚目の偏光板Yで遮断されます。
これを光子の場合で考えると以下になります。
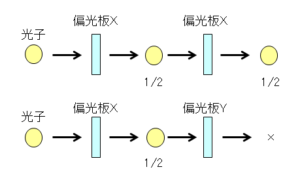
1枚目の偏光板Xを通過する光子の割合は1/2となります。1枚目の偏光板Xを通過した光子は、2枚目が偏光板が偏光板Xの場合は全て通過し、偏光板Yの場合は全て遮断されます。
一般に、ある光子の偏光の方向と偏光板の方向が $\theta$ ずれていた場合、偏光板を通過する光子の割合は $\cos^2\theta$ であることが知られています。そのため、偏光していない光子が偏光板を通過する確率は、これの平均を取った値(1/2)になります。
$$\frac{1}{2\pi}\int_0^{2\pi}\cos^2\theta d\theta=\frac{1}{2} -①$$
偏光は観測前に確定しているか?
Ca原子が励起状態から基底状態に戻るときに、2個の互いに直交した偏光をもつ光子を反対方向に放出することが知られています。この2個の光子を両側で検出する実験が以下になります。
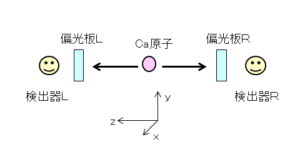
左側の偏光板(偏光板L)をx軸(横)方向、右側の偏光板(偏光板R)をy軸(縦)方向に設定すると、検出器Lで光子(以下、光子L)か検出された場合は、必ず検出器Rでも光子(以下、光子R)が検出されます。
量子力学では観測する前の量子状態は「分からない」とされていますが、ここで問題なのが、
- 人間に(量子力学で)分からないだけで、偏光は既に確定して”いる”
- 偏光は確定して”いない”
のどちらなのか、ということです。
仮設1:偏光は確定している
光子Lの偏光がx軸(偏光板Lの方向)に対して $\theta$ ほど傾いていたと”仮定”します。このとき、検出器Lで検出される確率は $\cos^2\theta$ となります。対になる光子Rは、y軸(偏光板Rの方向)に対して $\theta$ ほど傾いている”はず”なので、検出器Rで検出される確率は同じく $\cos^2\theta$ となります。
検出器Lと検出器Rで同時に検出される事象は、左右の確率事象が”独立”であれば、3/8の確率で発生します。これは以下のように計算されます。
$$\frac{1}{2\pi}\int_0^{2\pi}\cos^2\theta\cos^2\theta d\theta=\frac{3}{8}$$
仮設2:偏光は確定していない
この場合は、偏光板を通過した時点で、偏光が確定することになります。例えば、偏光板Lの通過が先に起こったとすると、偏光板Lを通過した時点で光子Lの偏光がx軸方向に確定し、それに伴い、光子Rの偏光がy軸方向に確定します。
光子Lが偏光板Lを通過する確率は①より1/2であり、y軸方向に偏光した光子Rが偏光板Rを通過する確率は1であるため、検出器Lと検出器Rで同時に検出される事象は1/2の確率になります。
$$\frac{1}{2\pi}\int_0^{2\pi}\cos^2\theta d\theta=\frac{1}{2}$$
結論
結論を言うと、実験結果は仮説2になります。光子が観測される前は、2つの光子の状態は確定しておらず、片方の観測結果が、もう片方の状態に影響を及ぼす関係にあります。この状態のことを量子もつれと呼びます。
| 仮設 | 光子の偏光は観測前に | 双方で光子が検出される確率 | 実験 |
| 仮設1 | 確定している | 3/8 | × |
| 仮設2 | 確定していない | 1/2 | ○ |
量子もつれの状態から、観測によって状態が確定することを、波束の収縮(デコヒーレンス)と呼びます。
このとき、片方の光子の情報がもう片方の光子に伝わりますが、これは2つの光子がどれだけ離れていようと瞬時に起こるため、相対性理論と一見矛盾しているように思えます。これはEPRパラドックスと呼ばれています。




