正規分布とは
正規分布とは、平均値を中心としたデータの「バラつき」を表す分布です。ガウス分布、または、誤差分布とも呼ばれます。何かを測定するときのデータのバラつき（誤差）の他、動物の身長や降ってくる雨粒の大きさの分布など、経験的に正規分布に従うことが知られています。
正規分布は、平均値を $\mu$、標準偏差を $\sigma$ とした場合、以下の式で定義されます。
$$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp{\Big(-\frac{(x-\mu)^2}{2\sigma^2}\Big)}\equiv N(\mu,\sigma^2)$$
正規分布の標準化
特に、平均値を $\mu=0$、標準偏差を $\sigma=1$ と置いた場合、以下のように正規分布を標準化できます。
$$f(u)=\frac{1}{\sqrt{2\pi}}\exp{\Big(-\frac{u^2}{2}\Big)}=N(0,1^2)$$
$$u\equiv\frac{x-\mu}{\sigma}$$
正規分布の特徴
正規分布は、グラフの中央は平均値となり、最も高い値（最頻値）を示します。また、グラフは左右対称で、偏りがない形となります。
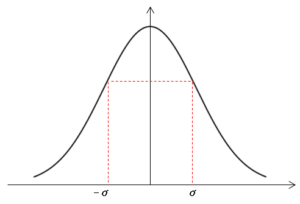
また、標準偏差が大きいほど、データのバラつきは大きく、グラフは平坦になります。標準偏差が同じであれば、それらのグラフは相似形になります。
さらに正規分布の式より、$x$ の値が $\pm n\sigma$（$n$ は整数）に含まれる割合（$f$ の面積）を求めることができます。例えば、$\pm\sigma$ の中に存在する $x$ の割合は約68％となります。
| $-\sigma\le x\le+\sigma$ | 68.2％ |
| $-2\sigma\le x\le+2\sigma$ | 95.4％ |
| $-3\sigma\le x\le+3\sigma$ | 99.7％ |
正規分布を導く
観測誤差の分布（正規分布）の形を、以下の仮定の下に求めます。
- 観測誤差は $n$ 個（$n\gg1$）の誤差要素から集積される。
- 各誤差要素は 1/2 の確率で $+\delta$ または $-\delta$ の値を持つ。
$n$ 個の誤差要素のうち $p$ 個が値 $+\delta$ を持つとき、残りの $n-p$ 個が値 $-\delta$ を持つとすると、このときの観測誤差 $x$ は、
$$x=(2p-n)\delta -①$$
この観測誤差が発生する確率分布を $f(x)$ とします。以下、この $f(x)$ を求めます。
確率分布の比
$n$ 個のうち、$p$ 個がプラスの値の場合の組み合わせの数（$C$）は以下になります。
$$C=\frac{n!}{(n-p)!p!}$$
同様に、$n$ 個のうち、$p+1$ 個がプラスの値の場合の観測誤差 $x’$ は、
$$x’=(2p-n+2)\delta=x+2\delta$$
その組み合わせの数 $C’$ は以下になります。
$$C’=\frac{n!}{(n-p-1)!(p+1)!}$$
このとき、２つの確率分布 $f(x)$ と $f(x’)=f(x+2\delta)$ の比は、組合せの数の比で表すことができます。尚、最後は $p\gg1$ としています。
$$\frac{f(x+2\delta)}{f(x)}=\frac{C’}{C}=\frac{n-p}{p+1}\simeq\frac{n-p}{p} -②$$
確率分布の形
次の $f(x)$ と $f(x+2\delta)$ の差分の式を定義します。
$$F\equiv\frac{f(x+2\delta)-f(x)}{f(x+2\delta)+f(x)} -③$$
この式に②を代入し、①を使って $p$ を消去すると、
$$F=\frac{n-2p}{n}=-\frac{x}{n\delta} -④$$
また、マクロリン展開
$$f(x+2\delta)\simeq f(x)+2\delta\frac{df}{dx}$$
を使うと、③は以下のように変形できます。尚、③の分母は $f(x)\simeq f(x+2\delta)$ と近似しています。
$$F=\frac{\delta}{f}\frac{df}{dx} -⑤$$
④と⑤より以下の微分方程式が得らます。
$$\frac{1}{f}\frac{df}{dx}=-\frac{x}{n\delta^2}$$
この微分方程式を解くと確率分布の形が求められます。ここで $A$ は比例定数です。
$$f(x)=A\exp{\Big(-\frac{x^2}{2n\delta^2}\Big)}$$
確率分布のバラつき
次に、$f(x)$ の変曲点の $x$ を求めます。変曲点とは、曲線の凸から凹、または、凹から凸に変化する点 “$x$” です。これは $f(x)$ の２階微分がゼロになる点として以下のように求められます。
$$\frac{d^2f(\sigma)}{dx^2}=0$$
この $x$ を改めて $\sigma$ と置きます。この $\sigma$ は標準偏差と呼ばれています。
$$\sigma=\delta\sqrt{n}$$
これにより、確率分布は以下になります。
$$f(x)=A\exp{\Big(-\frac{x^2}{2\sigma^2}\Big)}$$
規格化条件
最後は、定数 $A$ の求めるため、規格化を行います。以下のように $f(x)$ の $x$ の全領域での積分を１と置きます。
$$\int_{-\infty}^\infty f(x)dx=1$$
ここで以下の積分公式を使います。
$$\int_{-\infty}^\infty e^{-ax^2}dx=\sqrt{\frac{\pi}{a}} -⑥$$
これにより、$A=1/\sqrt{2\pi}\sigma$ が得られるため、確率分布が以下となることが分かります。
$$f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp{\Big(-\frac{x^2}{2\sigma^2}\Big)}$$
⑥を導く
積分 $I$ を以下で定義します。
$$I\equiv\int_{-\infty}^\infty e^{-x^2}dx$$
この $I$ を２乗すると、
$$I^2=\int_{-\infty}^\infty e^{-x^2}dx\int_{-\infty}^\infty e^{-y^2}dy=\int_{-\infty}^\infty\int_{-\infty}^\infty e^{-(x^2+y^2)}dxdy$$
これを極座標（$r,\theta$）に変換するっと、$x^2+y^2=r^2$ と $dxdy=rdrd\theta$ と書き換えることができるので、容易に積分することができます。
$$I^2=\int_0^{2\pi}d\theta\int_0^\infty re^{-r^2}dr=2\pi\left[-\frac{1}{2}e^{-r^2}\right]_0^\infty=\pi$$
これより、$I=\sqrt{\pi}$ が得られるため、
$$\int_{-\infty}^\infty e^{-x^2}dx=\sqrt{\pi}$$
さらに、$y\equiv\sqrt{a}x$ と置くと⑥が得られます。
$$\int_{-\infty}^\infty e^{-ax^2}dx=\int_{-\infty}^\infty e^{-y^2}\frac{dy}{\sqrt{a}}=\sqrt{\frac{\pi}{a}}$$
