量子ビット、量子コンピュータの回路（量子回路）を構成する素子です。量子コンピュータは、重ね合わせや量子もつれなどの量子力学的な現象を用いて、従来のコンピュータに比べ、特定の問題に対し高速な演算を実現することができます。
量子ビットの表現
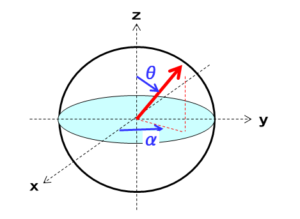
量子ビットの場合は、３次元の球面上の１点として表されます。従来のビット（以下、古典ビット）は「０」か「１」の２値ですが、それに対応する量子ビットは以下のように表されます。
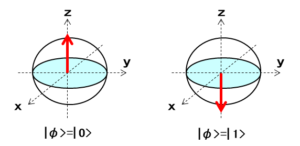
量子ビットの「０」はｚ軸のプラス向き、「１」はｚ軸のマイナス向きとして表され、ブラケット記号を用いてそれぞれ $\ket{0}$ と $\ket{1}$ と書きます。
量子ビットの特徴は、「０」と「１」の２つの状態の他に、その間の「重ね合わせ」の状態を取ることです。球面上の位置を表す変数である「$\theta$」と「$\alpha$」はそれぞれ、重ね合わせと位相に対応します。数式で表すと以下になります。
$$\ket{\phi}=\cos{\Big(\frac{\theta}{2}\Big)}\ket{0}+e^{i\alpha}\sin{\Big(\frac{\theta}{2}\Big)}\ket{1}$$
量子ビットの重ね合わせ
任意の量子ビットは「０」と「１」の重ね合わせの状態を持ちます。
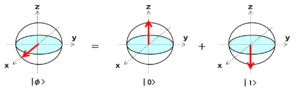
例えば、左辺の量子ビットはｘ軸のプラス方向 $(\theta,\alpha)=(\pi/2,0)$ に位置するため、以下で表されます。
$$\ket{\phi}=\frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1}$$
赤道面上の量子ビットは「０」と「１」が同じ割合で重なり合った状態で、この量子ビットを観測すると、50％の確率で「０」と「１」が現れます。
量子ビットの位相
量子ビットの位相は $\alpha$ で表されます。
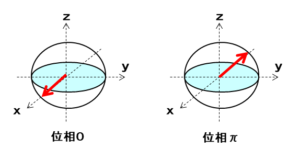
ｘ軸のプラスを向いた量子ビットの位相は０、ｘ軸のマイナスを向いた量子ビットの位相は $\pi$ になります。後者の量子ビット $(\theta,\alpha)=(\pi/2,\pi)$ は以下で表されます。
$$\ket{\phi}=\frac{1}{\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1}$$
複数の量子ビット
２量子ビットの場合（例えば、$\ket{01}$）は、それぞれの量子ビットが独立に $\ket{0}$ または $\ket{1}$ の状態を持つため、数学的には直積で表します。
$$\ket{01}=\ket{0}\otimes\ket{1}$$
このとき、各量子ビットが任意の量子ビット $\ket{\psi}$ とした場合、複素数 $\alpha,\beta$ によって、
$$\ket{\phi}=\alpha\ket{0}+\beta\ket{1}$$$$|\alpha|^2+|\beta|^2=1$$
で表されるとすると、
$$\ket{\phi}\otimes\ket{\phi}=(\alpha\ket{0}+\beta\ket{1})\otimes(\alpha\ket{0}+\beta\ket{1})$$
で計算されるため、任意の２量子ビットは、以下のような４つの状態の重ね合わせとして表すことができます。
$$\ket{\phi\phi}=\alpha^2\ket{00}+\alpha\beta\ket{01}+\beta\alpha\ket{10}+\beta^2\ket{11}$$
同様に考えると、３量子ビットは８つの状態、$n$ 量子ビットは $2^n$ の状態の重ね合わせを表現できます。この原理により、量子コンピュータでは高速な並列計算を行うことが可能になります。
