量子テレポーテーション
量子テレポーテーションとは、量子もつれのペアを作り、量子状態を遠隔地に転送する技術です。量子状態は読み出そうと(観測)すると、瞬時に固有状態に遷移してしまうため、盗み見(盗聴)することができません。量子暗号は、この原理の上に成り立っています。
量子回路
量子テレポーテーションの実現する量子回路は以下になります。ここでは、AからBへの量子状態($\ket{\psi}=c_0\ket{0}+c_1\ket{1}$)の伝達を考えます。量子状態(量子ビット)はAが2つ、Bが1つ持ち、$\ket{\psi}$ 以外の量子状態は $\ket{0}$ とします。
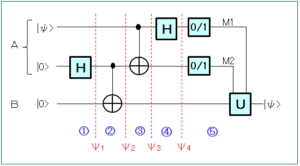
図中の[H]はアダマールゲート、[+]は制御NOTゲート、[0/1]は古典ゲート、[U]は制御ユニタリゲートを表します。それぞれの操作は後で説明します。
操作②($\Psi_1\to\Psi_2$)でAとBの間に量子もつれの状態を作り、操作⑤でAの量子状態を確定して、その情報を基にBはAが送ろうとした量子状態 $\psi$ を知ることができます。
量子状態の遷移
AからBへ量子状態 $\ket{\psi}$ が転送される操作を以下に説明します。
操作①
ここでは、量子ビット $\ket{0}$ に対してアダマールゲート[H]の操作を行います。
$$\ket{\Psi_1}=H\ket{0}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right)\left(\begin{array}{cc} 1 \\ 0 \end{array}\right)$$$$=\frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 \\ 1 \end{array}\right)=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})$$
ここで、量子ビットの行列表示は以下で定義されます。
$$\ket{0}\equiv\left(\begin{array}{cc} 1 \\ 0 \end{array}\right) , \ket{1}\equiv\left(\begin{array}{cc} 0 \\ 1 \end{array}\right)$$$$\ket{0}+\ket{1}\equiv\left(\begin{array}{cc} 1 \\ 1 \end{array}\right)$$
操作②
AとBの間で制御NOTゲートの操作を行い、量子もつれの状態を作ります。
$$\ket{\Psi_2}=\ket{\Psi_1}\otimes\ket{0}$$$$=\frac{1}{\sqrt{2}}(\ket{00}+\ket{10})=\frac{1}{\sqrt{2}}(\ket{00}+\ket{1\underline{1}})$$
最後の項で、制御ビットが「1」の場合は、下線部の通り反転「0→1」します。
尚、②で唯一AとBの間で演算を行いますが、お互いの状態($\ket{0}$)が分かっているため、独立して進めることができます。
操作③
Aの量子ビット間で制御NOTゲートの操作を行います。
$$\ket{\Psi_3}=\ket{\psi}\otimes\ket{\Psi_2}$$$$=\frac{1}{\sqrt{2}}\Big(c_0\ket{0}\otimes(\ket{00}+\ket{11})+c_1\ket{1}\otimes(\ket{\underline{1}0}+\ket{\underline{0}1})\Big)$$
最後の項で、制御ビットが「1」の場合は、下線部の通り反転します。
操作④
$\ket{\Psi_3}$ に対してアダマールゲートの操作を行います。
$$\ket{\Psi_4}=H\ket{\Psi_3}=\frac{1}{\sqrt{2}}\Big(c_0H\ket{0}\otimes(\ket{00}+\ket{11})$$$$+c_1H\ket{1}\otimes(\ket{10}+\ket{01})\Big)$$
結果は以下になります。下線部がアダーマルゲートの操作の結果です。
$$\ket{\Psi_4}=\frac{1}{2}\Big(c_0\underline{(\ket{0}+\ket{1})} \otimes(\ket{00}+\ket{11})$$$$+c_1\underline{(\ket{0}-\ket{1})} \otimes(\ket{10}+\ket{01})\Big)$$$$=\frac{1}{2}\Big(c_0(\ket{000}+\ket{011}+\ket{100}+\ket{111})$$$$+c_1(\ket{010}+\ket{001}-\ket{110}-\ket{101})\Big)$$
ここで、Aの量子ビット(左の2つ)でまとめると以下になります。
$$\ket{\Psi_4}=\frac{1}{2}\Big(\ket{00}\otimes(c_0\ket{0}+c_1\ket{1}) +\ket{01}\otimes(c_0\ket{1}+c_1\ket{0})$$$$+\ket{10}(c_0\ket{0}-c_1\ket{1}) +\ket{11}\otimes(c_0\ket{1}-c_1\ket{0})\Big)$$
この結果より、Aの量子ビットの状態($\ket{00},\ket{01},\ket{10},\ket{11}$)に対応して、Bの量子ビットが1つに定まることが分かります。
操作⑤
古典ゲート[0/1]では、Aの2つの量子ビットを読み出すこと(観測)で量子状態を確定させます。結果は、古典のビットと同様、「00」、「01」、「10」、「11」の4つのパターンが得られます。
そして、この4つのパターンのそれぞれに対し、Bの量子状態は決まっているため、適当なユニタリ演算を行うことで、常に $\ket{\psi}$ を取り出すことができます。
| [0/1] | $\ket{\psi_4}$ | ユニタリ演算 | Bの出力 |
| $\ket{00}$ | $c_0\ket{0}+c_1\ket{1}$ | なし | $c_0\ket{0}+c_1\ket{1}$ |
| $\ket{01}$ | $c_0\ket{1}+c_1\ket{0}$ | パウリXゲート | $c_0\ket{0}+c_1\ket{1}$ |
| $\ket{10}$ | $c_0\ket{0}-c_1\ket{1}$ | パウリZゲート | $c_0\ket{0}+c_1\ket{1}$ |
| $\ket{11}$ | $c_0\ket{1}-c_1\ket{0}$ | パウリ(X+Z)ゲート | $c_0\ket{0}+c_1\ket{1}$ |
以下で示されるように、どのパターンでも適当なユニタリ演算(パウリゲート)により、元のAの量子状態($\ket{\psi}$)をBで再現することができます。
- パターン「00」の場合は、操作は行いません。
- パターン「01」の場合は、パウリXゲート($U_X$)の操作を行います。
$$U_X(c_0\ket{1}+c_1\ket{0})=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{cc} c_1 \\ c_0 \end{array}\right)$$$$=\left(\begin{array}{cc} c_0 \\ c_1 \end{array}\right)=c_0\ket{0}+c_1\ket{1}$$ - パターン「10」の場合は、パウリZゲート($U_Z$)の操作を行います。
$$U_Z(c_0\ket{0}-c_1\ket{1})=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)\left(\begin{array}{cc} c_0 \\ -c_1 \end{array}\right)$$$$=\left(\begin{array}{cc} c_0 \\ c_1 \end{array}\right)=c_0\ket{0}+c_1\ket{1}$$ - パターン「11」の場合は、パウリXゲートとパウリZゲートの操作を行います。
$$U_ZU_X(c_0\ket{1}-c_1\ket{0})=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{cc} -c_1 \\ c_0 \end{array}\right)$$$$=\left(\begin{array}{cc} c_0 \\ c_1 \end{array}\right)=c_0\ket{0}+c_1\ket{1}$$




