変分法とは
変分法とは、汎関数が極値となるための関数を求める手法です。これは、関数を $y(x)$ 、汎関数を $f(x,y,y’)$ とすると、汎関数のある領域での積分が停留値を持つ条件として求められます。
$$I\equiv\int_a^bf(x,y,y’)dx -①$$
このとき、$x=a$ と $x=b$ では $y$ の値を固定し、その間の $x$ に対する $y$ の値を変化させます。$I$ が停留値を持つための条件 $\delta I=0$ は、以下のオイラーの微分方程式を解くことと同値になります。
$$\frac{\partial f}{\partial y}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’}\Big)=0 -②$$
②を導く
①の微小変位を取ると、
$$\delta I=\int_a^b\Big(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y’}\delta y’\Big)dx -(1)$$
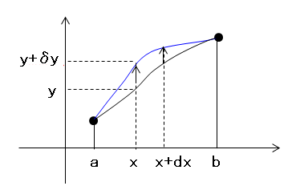
ここで、$x$ での $y$ の微小変位を $\delta y$ とすると、この微小変位の $x\to x+dx$ での値は、
$$\delta y(x+dx)=\delta y(x)+\frac{d(\delta y)}{dx}dx=\delta y(x)+d(\delta y) -(2)$$
一方、$x+dx$ での $y$ の値は、
$$y(x+dx)=y(x)+\frac{dy}{dx}dx=y(x)+dy$$
これの微小変位を取ると、
$$\delta y(x+dx)=\delta y(x)+\delta(dy) -(3)$$
(1)と(2)は等しくあるべきなので、$d(\delta y)=\delta(dy)$ となり、これを(1)の第2項に代入すると、
$$\delta I=\int_a^b\Big(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y’}\frac{d(\delta y)}{dx}\Big)dx$$
第2項に部分積分を行い、$x=a$ と $x=b$ で $\delta y=0$ という仮定を使うと、
$$\delta I=\int_a^b\frac{\partial f}{\partial y}\delta ydx+\Big[\frac{\partial f}{\partial y’}\delta y\Big]_a^b-\int_a^b\frac{d}{dx}\Big(\frac{\partial f}{\partial y’}\Big)\delta ydx$$$$=\int_a^b\Big[\frac{\partial f}{\partial y}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’}\Big)\Big]\delta ydx$$
任意の $\delta y$ で $\delta I=0$ となるためには、この被積分関数が0になる必要があるため②が得られます。
複数変数を含む場合
2変数 $x_1,x_2$ を含む汎関数の場合、
$$I\equiv\int_a^bf(x_1,x_2,y,y^{(1)},y^{(2)})dx_1dx_2$$$$y^{(1)}\equiv\frac{\partial y}{\partial x_1} , y^{(2)}\equiv\frac{\partial y}{\partial x_2}$$
オイラーの微分方程式は以下で表されます。
$$\frac{\partial f}{\partial y}-\frac{\partial}{\partial x_1}\Big(\frac{\partial f}{\partial y^{(1)}}\Big)-\frac{\partial}{\partial x_2}\Big(\frac{\partial f}{\partial y^{(2)}}\Big)=0 -③$$
③を導く
$I$ の微小変位を取り、同様に部分積分を行うと、
$$\delta I=\int_a^b\Big(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y^{(1)}}\delta y^{(1)}+\frac{\partial f}{\partial y^{(2)}}\delta y^{(2)}\Big)dx_1dx_2$$$$=\int_a^b\Big[\frac{\partial f}{\partial y}-\frac{\partial}{\partial x_1}\Big(\frac{\partial f}{\partial y^{(1)}}\Big)-\frac{\partial}{\partial x_2}\Big(\frac{\partial f}{\partial y^{(2)}}\Big)\Big]\delta ydx_1dx_2$$
任意の $\delta y$ で $\delta I=0$ となるためには、この被積分関数が0になる必要があるため③が得られます。
複数関数を含む場合
2関数 $y_1,y_2$ を含む汎関数の場合、
$$I\equiv\int_a^bf(x,y_1,y_2,y’_1,y’_2)dx$$
オイラーの微分方程式は以下で表されます。
$$\frac{\partial f}{\partial y_1}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’_1}\Big)=0 -④$$$$\frac{\partial f}{\partial y_2}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’_2}\Big)=0 -④$$
④を導く
$I$ の微小変位を取り、同様に部分積分を行うと、
$$\delta I=\int_a^b\Big(\frac{\partial f}{\partial y_1}\delta y_1+\frac{\partial f}{\partial y’_1}\delta y’_1+\frac{\partial f}{\partial y_2}\delta y_2+\frac{\partial f}{\partial y’_2}\delta y’_2\Big)dx$$$$=\int_a^b\Big[\frac{\partial f}{\partial y_1}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’_1}\Big)\Big]\delta y_1dx+\int_a^b\Big[\frac{\partial f}{\partial y_2}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’_2}\Big)\Big]\delta y_2dx$$
任意の $\delta y_1,\delta y_2$ で $\delta I=0$ となるためには、それぞれの被積分関数が0になる必要があるため④が得られます。
高階微分を含む場合
2階微分を含む汎関数の場合、
$$I\equiv\int_a^bf(x,y,y’,y^{”})dx$$
オイラーの微分方程式は以下で表されます。
$$\frac{\partial f}{\partial y}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’}\Big)+\frac{d^2}{dx^2}\Big(\frac{\partial f}{\partial y^{”}}\Big)=0 -⑤$$
⑤を導く
$I$ の微小変位を取り、同様に部分積分を行うと、
$$\delta I=\int_a^b\Big(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y’}\delta y’+\frac{\partial f}{\partial y^{”}}\delta y^{”}\Big)dx$$
右辺の第3項の積分については、
$$\int_a^b\frac{\partial f}{\partial y^{”}}\delta y^{”}dx=\int_a^b\frac{\partial f}{\partial y^{”}}\frac{d^2(\delta y)}{dx^2}dx$$$$=\Big[\frac{\partial f}{\partial y^{”}}\frac{d(\delta y)}{dx}\Big]_a^b-\int_a^b\frac{d}{dx}\Big(\frac{\partial f}{\partial y^{”}}\Big)\frac{d(\delta y)}{dx}dx$$$$=-\Big[\frac{d}{dx}\Big(\frac{\partial f}{\partial y^{”}}\Big)\delta y\Big]_a^b+\int_a^b\frac{d^2}{dx^2}\Big(\frac{\partial f}{\partial y^{”}}\Big)\delta ydx$$$$=\int_a^b\frac{d^2}{dx^2}\Big(\frac{\partial f}{\partial y^{”}}\Big)\delta ydx$$
従って、
$$\delta I=\int_a^b\Big[\frac{\partial f}{\partial y}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’}\Big)+\frac{d^2}{dx^2}\Big(\frac{\partial f}{\partial y^{”}}\Big)\Big]\delta ydx$$
任意の $\delta y$ で $\delta I=0$ となるためには、この被積分関数が0になる必要があるため⑤が得られます。
パラメタを含む場合
パラメタ $\alpha$ を含む汎関数の場合、
$$I\equiv\int_a^bf(x,y,y’,\alpha)dx$$
オイラーの微分方程式は以下で表されます。
$$\frac{\partial f}{\partial y}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’}\Big)=0 -⑥$$$$\frac{\partial f}{\partial\alpha}=0 -⑥$$
⑥を導く
$I$ の微小変位を取り、同様に部分積分を行うと、
$$\delta I=\int_a^b\Big(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y’}\delta y’+\frac{\partial f}{\partial\alpha}\delta\alpha\Big)dx$$$$=\int_a^b\Big[\frac{\partial f}{\partial y}-\frac{d}{dx}\Big(\frac{\partial f}{\partial y’}\Big)\Big]\delta ydx+\int_a^b\frac{\partial f}{\partial\alpha}\delta\alpha dx$$
任意の $\delta y,\delta\alpha$ で $\delta I=0$ となるためには、それぞれの被積分関数が0になる必要があるため⑥が得られます。