ガウスの発散定理とは
ガウスの定理とは、ベクトル場 $A=(A_x,A_y,A_z)$ の任意の閉曲面上の面積分が、ベクトル場の発散(Divergence)の体積分に一致することを述べたものです。
$$\oint{\bf A}\cdot d{\bf S}=\int_V\nabla\cdot{\bf A}dV$$
ここで、ナブラ記号は以下で定義されます。
$$\nabla\equiv\Big(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\Big)$$
ガウスの発散定理を導く
以下のような微小立方体を考え、直感的に求めてみます。
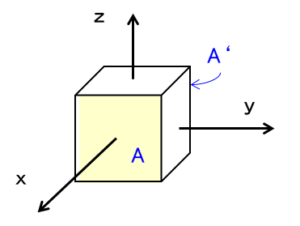
x軸に垂直な面( $yz$ 面)は2つありますが、手前(プラス側)の面に垂直な単位ベクトルを ${\bf n}_x$ 、奥(マイナス側)の面に垂直な単位ベクトルを ${\bf n’}_x$ とします。他の4つの $zx$ 面と $xy$ 面も同様に考えると、立方体上の積分は6つの面の和で表すことができます。
$${\bf A}\cdot d{\bf S}={\bf A}\cdot({\bf n}_x+{\bf n’}_x+{\bf n}_y+{\bf n’}_y+{\bf n}_z+{\bf n’}_z)dS -(1)$$
簡単のため2つの $yz$ 面(1項目と2項目)を考えます。それぞれのベクトル場を ${\bf A}$ 、${\bf A}’$ とすると以下になります。
$${\bf A}\cdot({\bf n}_x+{\bf n’}_x)dS=(A_x-A’_x)dydz=\frac{A_x-A’_x}{\Delta x}\Delta xdydz$$
ここで $\Delta x$ は十分に小さいとすると以下になります。
$$\frac{A_x-A’_x}{\Delta x}\Delta xdydz=\frac{\partial A_x}{\partial x}dxdydz$$
$zx$ 面と $xy$ 面も同様に考えると、
$${\bf A}\cdot({\bf n}_y+{\bf n’}_y)dS=(A_y-A’_y)dzdx=\frac{\partial A_y}{\partial y}dxdydz$$$${\bf A}\cdot({\bf n}_z+{\bf n’}_z)dS=(A_z-A’_z)dxdy=\frac{\partial A_z}{\partial z}dxdydz$$
(1)は以下になります。
$${\bf A}\cdot d{\bf S}=\left(\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}\right)dxdydz=\nabla\cdot{\bf A}dV$$
これにより、ガウスの発散定理が導けたことが分かります。




