効率的フロンティアとは

効率的フロンティア

効率的フロンティアとは、投資家が選択できるリターンとリスクの組み合わせ（投資機会集合）において、同じリスクに対しリターンが最大となる点の集合です。

複数のリスク資産から構成されるポートフォリオの投資機会集合は、下図の青い曲線ような左に凸の曲線の内側として表されます。

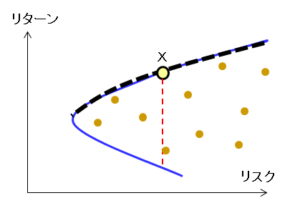
例えば、同じリスクのポートフォリオ（赤い点線）を考えると、投資家はよりリターンの高いポートフォリオ（点Ｘ）を選択します。これより、投資家の満足度が最も高いのは、投資機会集合の上端（太い点線）として表されます。これを効率的フロンティアと呼んでいます。

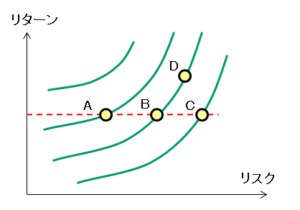
効用無差別曲線とは、その曲線上では投資家の満足度（リターン）が等しくなる曲線です。効用無差別曲線は下図の緑の曲線で表されます。

尚、同じリターンであれば、よりリスクの低い投資を好む投資家を「リスク回避者」と呼びますが、現代ポートフォリオ理論では「リスク回避者」であることを前提としています。

例えば、資産Ａ、資産Ｂ、資産Ｃはどれもリターンが等しくなりますが、リスク回避者であれば資産Ａを選択します。つまり、効用無差別曲線は左になるほど投資家の満足度は高くなります。

尚、資産Ｂと資産Ｄは同じ効用無差別曲線にあるため、投資家の満足度は等しいとされます。どちらを選択するかは、ローリスク・ローリターン（資産Ｂ）か、ハイリスク・ハイリターン（資産Ｄ）の選択に成ります。

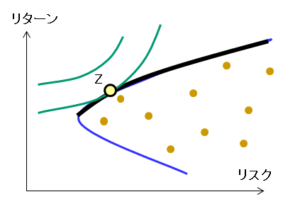
最適ポートフォリオとは、投資家の満足度が最大になるポートフォリオです。最適ポートフォリオは、効率的フロンティア（太線）と効用無差別曲線（緑の曲線）の接点（点Ｚ）として表されます。

接点ポートフォリオとは、ポートフォリオに無リスク資産を組み込んだ場合に、最もリターンが高くなるポートフォリオ（点Ｙ）です。

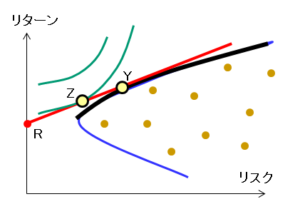
国債など無リスク資産は、縦軸上の点Ｒとして表されます。リスク資産と無リスク資産を組み合わせた効率的フロンティアは、点Ｒと点Ｙを結ぶ線（赤い直線）で表されます。この効率的フロンティアが曲線ではなく直線になるのは、無リスク資産が標準偏差０であるため、ポートフォリオの標準偏差が加重平均になるためです。

従って、無リスク資産を含めた場合の最適ポートフォリオは、この効率的フロンティアと効用無差別曲線との接点（点Ｚ）として表されます。

無リスク資産がない場合とある場合の最適ポートフォリオを比べると、無リスク資産がある場合の最適ポートフォリオの方が、同じリターンに対するリスクが小さい（点の位置が左にずれる）ことが分かります。

トービンの分離定理とは、リスク資産と無リスク資産からなるポートフォリオにおいて、リスク資産の中の投資割合（接点ポートフォリオ）と、リスク資産と無リスク資産の投資割合（最適ポートフォリオ）は、別々に判断されるということを言います。

これは、接点ポートフォリオが各資産のリスクとリターンによって自動的に決まるのに対し、最適ポートフォリオは投資家の好み（効用無差別曲線）により決まるからです。