量子ビット
量子ビットは、量子コンピュータの回路（量子回路）を構成する素子です。量子コンピュータは、重ね合わせや量子もつれなどの量子力学的な現象を用いて、従来のコンピュータに比べ、特定の問題に対し高速な演算を実現することができます。
量子ビットの表現
量子ビットの場合は、３次元の球面上の１点として表されます。従来のビット（以下、古典ビット）は「０」か「１」の２値ですが、それに対応する量子ビットは以下のように表されます。
量子ビットの「０」はｚ軸のプラス向き、「１」はｚ軸のマイナス向きとして表され、ブラケット記号を用いてそれぞれ $\ket{0}$ と $\ket{1}$ と書きます。
量子ビットの特徴は、「０」と「１」の２つの状態の他に、その間の「重ね合わせ」の状態を取ることです。球面上の位置を表す変数である「$\theta$」と「$\alpha$」はそれぞれ、重ね合わせと位相に対応します。数式で表すと以下になります。
$$\ket{\phi}=\cos{\Big(\frac{\theta}{2}\Big)}\ket{0}+e^{i\alpha}\sin{\Big(\frac{\theta}{2}\Big)}\ket{1} -①$$
量子ビットの重ね合わせ
任意の量子ビットは「０」と「１」の重ね合わせの状態を持ちます。
例えば、左辺の量子ビットはｘ軸のプラス方向 $(\theta,\alpha)=(\pi/2,0)$ に位置するため、以下で表されます。
$$\ket{\phi}=\frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1}$$
赤道面上の量子ビットは「０」と「１」が同じ割合で重なり合った状態で、この量子ビットを観測すると、50％の確率で「０」と「１」が現れます。
量子ビットの位相
量子ビットの位相は $\alpha$ で表されます。
ｘ軸のプラスを向いた量子ビットの位相は０、ｘ軸のマイナスを向いた量子ビットの位相は $\pi$ になります。後者の量子ビット $(\theta,\alpha)=(\pi/2,\pi)$ は以下で表されます。
$$\ket{\phi}=\frac{1}{\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1}$$
量子ビットの計算
量子ビットの規格化
各量子ビットが①のように表される任意の量子ビット $\ket{\phi}$ であるとした場合、一般に複素数 $\alpha,\beta$ によって、
$$\ket{\phi}\equiv\alpha\ket{0}+\beta\ket{1}$$
規格化条件は以下になります。
$$|\alpha|^2+|\beta|^2=1$$
量子ビットの内積
２つの量子ビットを以下で表すと、
$$\ket{\phi_1}\equiv\alpha_1\ket{0}+\beta_1\ket{1}$$$$\ket{\phi_2}\equiv\alpha_2\ket{0}+\beta_2\ket{1}$$
このとき、
$$\braket{0|0}=\braket{1|1}=1$$$$\braket{0|1}=\braket{1|0}=0$$
より、量子ビットの内積は以下になります。
$$\braket{\phi_1|\phi_2}=\alpha_1^*\alpha_2+\beta_1^*\beta_2$$
量子ビットの直積
２量子ビットの場合（例えば、$\ket{01}$）は、それぞれの量子ビットが独立に $\ket{0}$ または $\ket{1}$ の状態を持つため、数学的には直積で表します。
$$\ket{01}=\ket{0}\otimes\ket{1}$$
３量子ビット以上についても同様の考え方になります。
量子ビットの重ね合わせ
任意の量子ビットの直積は、
$$\ket{\phi}\otimes\ket{\phi}=(\alpha\ket{0}+\beta\ket{1})\otimes(\alpha\ket{0}+\beta\ket{1})$$
この場合、以下のような４つの状態の重ね合わせとして表すことができます。
$$\ket{\phi\phi}=\alpha^2\ket{00}+\alpha\beta\ket{01}+\beta\alpha\ket{10}+\beta^2\ket{11}$$
同様に考えると、３量子ビットは８つの状態、$n$ 量子ビットは $2^n$ の状態の重ね合わせを表現できます。この原理により、量子コンピュータでは高速な並列計算を行うことが可能になります。
量子ゲート
量子ゲートとは、量子ビット（量子状態）に対する操作の手順を表します。量子回路では、量子ビットに量子ゲートを作用させることで演算を行います。以下は主な量子ゲートについて紹介します。
ユニタリゲート
回転ゲートとは、量子ビットをある軸の周りに一定の角度回転させる操作です。例えば、ｙ軸周りに90度回転させる場合は以下の図になります。
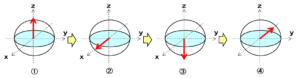
①（$\ket{0}$）に対して90度の回転を２回行うと③（$\ket{1}$）になります。さらに、④に対し90度の回転を２回行うと元の①に戻ります。
一般に量子ビットは $\ket{0}$ と $\ket{1}$ の重ね合わせになるため、
$$\ket{\psi}=c_0\ket{0}+c_1\ket{1} \to \ket{\psi’}=c’_0\ket{0}+c’_1\ket{1}$$
ユニタリゲートによる変換は２階の行列 $U$ で表されます。
$$\ket{\psi’}=U\ket{\psi}$$
$$\left(\begin{array}{cc} c’_0 \\ c’_1 \end{array}\right)=U\left(\begin{array}{cc} c_0 \\ c_1 \end{array}\right)$$
主なユニタリゲートは、パウリゲートとアダマールゲートです。
パウリゲート
パウリゲート $U_x,U_y,U_z$ は、パウリの３つのスピン行列と同じ働きをするユニタリゲートです。
$$\ket{\psi’}=U_x\ket{\psi}=\left(\begin{array}{cc} 0 & 1 \\
1 & 0 \end{array}\right)\ket{\psi}$$$$\ket{\psi’}=U_y\ket{\psi}=\left(\begin{array}{cc} 0 & -i \\
i & 0 \end{array}\right)\ket{\psi}$$$$\ket{\psi’}=U_z\ket{\psi}=\left(\begin{array}{cc} 1 & 0 \\
0 & -1 \end{array}\right)\ket{\psi}$$
アダマールゲート
アダマールゲート $U_H$ は、ｘ軸とｚ軸の中間の軸を中心に回転させる変換に相当します。
$$\ket{\psi’}=U_H\ket{\psi}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc} 1 & 1 \\
1 & -1 \end{array}\right)\ket{\psi}$$
このとき、各ビットは以下のように変換されます。
$$\ket{0} \to \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})$$$$\ket{1} \to \frac{1}{\sqrt{2}}(\ket{0}-\ket{1})$$
制御NOTゲート
制御NOTゲート（CNOT）は、制御ビットと信号ビットと呼ばれる２つの量子ビットの入力に対して、２つの量子ビットを出力します。
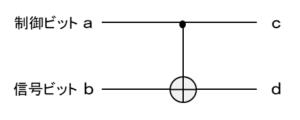
制御ビットが「１」（オン）の場合に信号ビットを反転させ、「０」（オフ）の場合は信号ビットは変化しません。制御NOTゲートの真理値表は以下になります。
| a | b | c | d |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 |
一般に量子ビットは $\ket{0}$ と $\ket{1}$ の重ね合わせになるため、入力側ビットを、
$$\ket{a}=c_0\ket{0}+c_1\ket{1}$$$$\ket{b}=c_2\ket{0}+c_3\ket{1}$$
である場合、２量子ビットの重ね合わせとして表されるため、
$$(c_0\ket{0}+c_1\ket{1})\otimes(c_2\ket{0}+c_3\ket{1})$$$$=c_0c_2\ket{00}+c_0c_3\ket{01}+c_1c_2\ket{10}+c_1c_3\ket{11}$$
この状態に対し制御NOTゲートを通すと、制御ビットが「１」のときに信号ビットが反転するため、この右辺は以下の下線部のように変換されます。
$$c_0c_2\ket{00}+c_0c_3\ket{01}+c_1c_2\ket{1\underline{1}}+c_1c_3\ket{1\underline{0}}$$
制御回転ゲート
制御回転ゲートとは、制御ビットが $\ket{0}$ の場合は、信号ビットはそのまま通過し、制御ビットが $\ket{1}$ の場合は、信号ビットは以下のような変換を行う量子ゲートです。
$$\ket{0} \to \ket{0}$$$$\ket{1} \to e^{2\pi i/2^n}\ket{1}$$
制御ユニタリゲート
制御ユニタリゲートとは、制御ビットによって制御されたユニタリ変換です。制御ビットが $\ket{0}$ の場合は、信号ビットはそのまま通過し、制御ビットが $\ket{1}$ の場合は、信号ビットはユニタリ変換されます。
尚、制御NOTゲートは、制御ユニタリゲートでパウリゲート $U_x$ の場合に相当します。
$$\ket{\psi’}=U_x\ket{\psi}=\left(\begin{array}{cc} 0 & 1 \\
1 & 0 \end{array}\right)\ket{\psi}$$
逆量子フーリエ変換
逆量子フーリエ変換は、量子フーリエ変換の逆変換を量子回路で実現した量子ゲートです。量子位相推定（位数計算）などで利用されます。
