量子フーリエ変換とは - 理数の散策路

量子フーリエ変換
量子回路

量子フーリエ変換

量子フーリエ変換とは、信号処理で使われる離散フーリエ変換を量子回路上に実装したものです。

離散フーリエ変換は、離散的（単位時間毎）に $N$ 回だけ物理量 $x_{j}$ （ $j = 0, 1, \dots, N - 1$ ）を測定した場合、以下で表すことができます。

$x_{j} = \frac{1}{\sqrt{N}} \sum_{k = 0}^{N - 1} X_{k} e^{2 π i k j / N}$

量子フーリエ変換は、この離散フーリエ変換（ $x_{j} \to X_{k}$ ）を用いて、以下の変換で定義されます。

$\sum_{j = 0}^{N - 1} x_{j} | j ⟩ \to \sum_{k = 0}^{N - 1} X_{k} | k ⟩$

このとき、状態ベクトルは以下のように変換されます。

$| j ⟩ \to \frac{1}{\sqrt{N}} \sum_{k = 0}^{N - 1} e^{2 π i k j / N} | k ⟩ － ①$

量子フーリエ変換を量子回路で実現するため、状態ベクトル $| j ⟩$ を量子ビットで表す必要があります。 $N = 2^{n}$ とし、10進法である $j$ を２進法で表すと、

$j = j_{1} \cdot 2^{n - 1} + j_{2} \cdot 2^{n - 2} + \dots + j_{n} \cdot 2^{0} － ②$

状態ベクトルは以下で置き替えます。

$| j ⟩ = | j_{1} j_{2} \dots j_{n} ⟩ = | j_{1} ⟩ \otimes | j_{2} ⟩ \otimes \dots \otimes | j_{n} ⟩$

n=4 の場合の変換

以下に、 $n = 4$ （ $N = 2^{4}$ ）として①を計算すると以下のようになります。

$| j ⟩ \to \frac{1}{\sqrt{2^{4}}} \sum_{k = 0}^{2^{4} - 1} e^{2 π i k j / 2^{4}} | k ⟩$ $= \frac{1}{4} (| 0 ⟩ + e^{2 π i (0. j_{4})} | 1 ⟩) \otimes (| 0 ⟩ + e^{2 π i (0. j_{3} j_{4})} | 1 ⟩)$ $\otimes (| 0 ⟩ + e^{2 π i (0. j_{2} j_{3} j_{4})} | 1 ⟩) \otimes (| 0 ⟩ + e^{2 π i (0. j_{1} j_{2} j_{3} j_{4})} | 1 ⟩) － ③$

③を導く

$k$ を２進法に書き替えると、

$| j ⟩ \to \frac{1}{4} \sum_{k_{1} = 0}^{1} \sum_{k_{2} = 0}^{1} \sum_{k_{3} = 0}^{1} \sum_{k_{4} = 0}^{1} e^{2 π i j (k_{1} 2^{3} + k_{2} 2^{2} + k_{3} 2^{1} + k_{4} 2^{0}) / 2^{4}} | k_{1} k_{2} k_{3} k_{4} ⟩$

指数部分を分解し、それぞれ和を取ると、

$= \frac{1}{4} \sum_{k_{1} = 0}^{1} e^{2 π i j k_{1} / 2} | k_{1} ⟩ \otimes \sum_{k_{2} = 0}^{1} e^{2 π i j k_{2} / 2^{2}} | k_{2} ⟩$ $\otimes \sum_{k_{3} = 0}^{1} e^{2 π i j k_{3} / 2^{3}} | k_{3} ⟩ \otimes \sum_{k_{4} = 0}^{1} e^{2 π i j k_{4} / 2^{4}} | k_{4} ⟩$

$= \frac{1}{4} (| 0 ⟩ + e^{2 π i j / 2} | 1 ⟩) \otimes (| 0 ⟩ + e^{2 π i j / 2^{2}} | 1 ⟩)$ $\otimes (| 0 ⟩ + e^{2 π i j / 2^{3}} | 1 ⟩) \otimes (| 0 ⟩ + e^{2 π i j / 2^{4}} | 1 ⟩)$

ここで、各指数部分に②を代入すると、

$e^{2 π i j / 2} = e^{2 π i (j_{1} 2^{2} + j_{2} 2 + j_{3} + j_{4} / 2)} = e^{2 π i (j_{4} / 2)} = e^{2 π i (0. j_{4})}$

$e^{2 π i j / 2^{2}} = e^{2 π i (j_{1} 2 + j_{2} + j_{3} / 2 + j_{4} / 2^{2})} = e^{2 π i (j_{3} / 2 + j_{4} / 2^{2})} = e^{2 π i (0. j_{3} j_{4})}$

$e^{2 π i j / 2^{3}} = e^{2 π i (j_{1} + j_{2} / 2 + j_{3} / 2^{2} + j_{4} / 2^{3})} = e^{2 π i (j_{2} / 2 + j_{3} / 2^{2} + j_{4} / 2^{3})} = e^{2 π i (0. j_{2} j_{3} j_{4})}$

$e^{2 π i j / 2^{4}} = e^{2 π i (j_{1} / 2 + j_{2} / 2^{2} + j_{3} / 2^{3} + j_{4} / 2^{4})} = e^{2 π i (0. j_{1} j_{2} j_{3} j_{4})}$

これらより、③の結果が導かれます。

量子回路

量子フーリエ変換を実現する量子回路は以下になります。「 $H$ 」はアダマールゲート、「 $R_{m}$ 」は制御回転ゲートを表します。

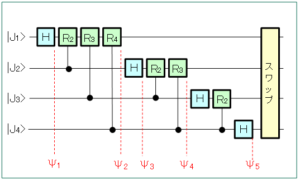
アダマールゲートは、量子ビットに対し以下の変換を行います。

$| 0 ⟩ \to \frac{1}{\sqrt{2}} (| 0 ⟩ + | 1 ⟩)$

$| 1 ⟩ \to \frac{1}{\sqrt{2}} (| 0 ⟩ - | 1 ⟩)$

制御回転ゲートは、制御ビットが $| 0 ⟩$ のときはそのまま通し、 $| 1 ⟩$ のときは以下の変換を行います。

$| 0 ⟩ \to | 0 ⟩$

$| 1 ⟩ \to e^{2 π i / 2^{m}} | 1 ⟩$

最後のスワップゲートは、以下のような量子ビットの入れ替えを行います。

$| j_{1} ⟩ \otimes | j_{2} ⟩ \otimes | j_{3} ⟩ \otimes | j_{4} ⟩ \to | j_{4} ⟩ \otimes | j_{3} ⟩ \otimes | j_{2} ⟩ \otimes | j_{1} ⟩$

n=4 の場合の動作

$j_{1}$ ビットが各ゲートを通過（ $H \to R_{2} \to R_{3} \to R_{4}$ ）した場合を計算します。まず、アダマールゲートで変換すると、

$| j_{1} j_{2} j_{3} j_{4} ⟩ = \frac{1}{\sqrt{2}} (| 0 ⟩ + e^{2 π i (0. j_{1})} | 1 ⟩) \otimes | j_{2} j_{3} j_{4} ⟩$

$R_{2}$ ゲートで変換すると、

$= \frac{1}{\sqrt{2}} (| 0 ⟩ + e^{2 π i (0. j_{1} j_{2})} | 1 ⟩) \otimes | j_{2} j_{3} j_{4} ⟩$

続けて $R_{3}, R_{4}$ で変換すると、

$= \frac{1}{\sqrt{2}} (| 0 ⟩ + e^{2 π i (0. j_{1} j_{2} j_{3} j_{4})} | 1 ⟩) \otimes | j_{2} j_{3} j_{4} ⟩$

$j_{2}$ ビットが各ゲートを通過（ $H \to R_{2} \to R_{3}$ ）した場合を計算すると同様に、

$= \frac{1}{\sqrt{2}} (| 0 ⟩ + e^{2 π i (0. j_{1} j_{2} j_{3} j_{4})} | 1 ⟩) \otimes \frac{1}{\sqrt{2}} (| 0 ⟩ + e^{2 π i (0. j_{2} j_{3} j_{4})} | 1 ⟩) \otimes | j_{3} j_{4} ⟩$

従って $j_{3}$ ビットと $j_{4}$ ビットも計算すると以下になります。

$= \frac{1}{\sqrt{2^{4}}} (| 0 ⟩ + e^{2 π i (0. j_{1} j_{2} j_{3} j_{4})} | 1 ⟩) \otimes (| 0 ⟩ + e^{2 π i (0. j_{2} j_{3} j_{4})} | 1 ⟩)$ $\otimes (| 0 ⟩ + e^{2 π i (0. j_{3} j_{4})} | 1 ⟩) \otimes (| 0 ⟩ + e^{2 π i (0. j_{4})} | 1 ⟩)$

最後にスワップゲートで変換すると、 $j_{1}$ と $j_{4}$ 、 $j_{2}$ と $j_{3}$ のビットが入れ替わるため、③が得られます。

$= \frac{1}{\sqrt{2^{4}}} (| 0 ⟩ + e^{2 π i (0. j_{4})} | 1 ⟩) \otimes (| 0 ⟩ + e^{2 π i (0. j_{3} j_{4})} | 1 ⟩)$ $\otimes (| 0 ⟩ + e^{2 π i (0. j_{2} j_{3} j_{4})} | 1 ⟩) \otimes (| 0 ⟩ + e^{2 π i (0. j_{1} j_{2} j_{3} j_{4})} | 1 ⟩)$