ニューラルネットワーク
ニューラルネットワークとは、脳機能の特性に類似した数理的モデルです。ニューロン(神経細胞)とシナプス(ニューロンの接合部分)からネットワークを形成し、学習によってシナプスの結合強度を変化させ、問題解決を行います。
ネットワーク関数
ニューロンを配置する層は、入力層、中間層、出力層などに分かれています。以下は、中間層が1層の場合のモデルを取り上げます。
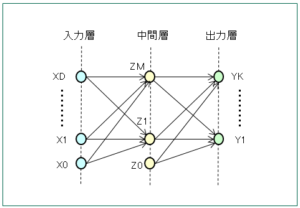
まず、入力層($x_0,x_1,\cdots,x_D$)から中間層($z_0,z_1,\cdots,z_M$)への伝播は以下の線形和で表します。
$$a_j=\sum_{i=0}^Dw^{(1)}_{ji}x_i , x_0=1 -①$$
$$z_j=h(a_j)$$
ここで、$w^{(1)}_{ji}$ は重みパラメタ、$w^{(1)}_{j0}$ はバイアスパラメタです。$a_j$ は活性と呼ばれ、活性化関数 $h$ で変換され中間層に渡されます。活性化関数には、$\tanh$ 関数や以下のロジスティックシグモイド関数などが使われます。
$$h(a_j)=\frac{1}{1+e^{-a_j}}$$
次に、中間層から出力層($y_0,y_1,\cdots,y_K$)への伝播は以下の線形和で表します。活性化関数 $\sigma$ にはロジスティックシグモイド関数などが使われます。
$$a_k=\sum_{j=0}^Mw^{(2)}_{kj}z_j , z_0=1 -②$$
$$y_k=\sigma(a_k)$$
①と②の合わせると、入力層から出力層への伝播は以下でまとめられます。
$$y_k(x,w)=\sigma\left(\sum_{j=0}^Mw_{kj}^{(2)}h\Big(\sum_{i=0}^Dw_{ji}^{(1)}x_i\Big)\right)$$
誤差の評価
誤差の評価により、ニューラルネットワークの重みパラメタ $w$ を求めます。具体的には、入力ベクトル ${\bf x}_n$ の集合に対する目標ベクトル ${\bf t}_n$ が与えられたとき、次の二乗和誤差を最小にする重みパラメタを求めることです。
$$E({\bf w})=\frac{1}{2}\sum_{n=1}^N|y({\bf x}_n,{\bf w})-{\bf t}_n|^2$$
この二乗和誤差を最小(極小)にするための条件は以下で表されます。
$$\nabla E({\bf w})=\sum\frac{\partial E}{\partial w_{ij}}=0 -③$$$$\frac{\partial^2E}{\partial w_{ij}^2}\gt0$$
誤差逆伝播法
誤差逆伝搬法(Backpropagation Method)とは、ニューラルネットワークを学習させる際に用いられるアルゴリズムです。中間層について、次のようなモデルを想定います。
$$z_j=h(a_j) , a_j=\sum_iw_{ji}^{(1)}x_i -④$$$$y_k=h(a_k) , a_k=\sum_jw_{kj}^{(2)}z_j -⑤$$
ここで、誤差 $\delta$ を以下で定義します。
$$\delta_j\equiv\frac{\partial E}{\partial a_j} -⑥$$
$$\delta_k\equiv\frac{\partial E}{\partial a_k}\cong y_k-t_k -⑦$$
誤差逆伝搬法の手順
誤差逆伝搬法の手順は以下になります。
- ④と⑤より、順伝播で全ての中間層と出力層の値を求める。
- ⑦より、出力層の誤差 $\delta_k$ を計算する。
- ⑧より、誤差 $\delta$ を逆伝搬させ、全ての中間層の誤差を求める。
$$\delta_j=\sum_k\delta_kw_{kj}^{(2)}h'(a_j) -⑧$$ - ⑨と⑩より、極小条件③を評価する。
$$\frac{\partial E}{\partial w_{ji}^{(1)}}=\delta_jx_i -⑨$$$$\frac{\partial E}{\partial w_{kj}^{(2)}}=\delta_kz_j -⑩$$
⑧の導出
まず、⑥と⑦より、
$$\delta_j=\sum_k\frac{\partial E}{\partial a_k}\frac{\partial a_k}{\partial a_j}=\sum_k\delta_k\frac{\partial a_k}{\partial a_j} -(1)$$
④と⑤より、
$$a_k=\sum_jw_{kj}^{(2)}h(a_j)$$
この両辺を $a_j$ で微分すると、
$$\frac{\partial a_k}{\partial a_j}=w_{kj}^{(2)}\frac{\partial h(a_j)}{\partial a_j}$$
これを(1)に代入すると、⑧が得られます。
⑨と⑩の導出
④より二乗和誤差 $E$ へは $a_j$ を通して依存することに着目すると、
$$\nabla E({\bf w})=\frac{\partial E}{\partial w_{ji}^{(1)}}=\frac{\partial E}{\partial a_j}\frac{\partial a_j}{\partial w_{ji}^{(1)}} -(2)$$
④の両辺を $w_{ji}$ で微分すると、
$$\frac{\partial a_j}{\partial w_{ji}^{(1)}}=x_i$$
これと⑥を(2)に代入すると、⑨が得られます。一方、⑩についても、(2)を以下のように書き換えると同様に得ることができます。
$$\nabla E({\bf w})=\frac{\partial E}{\partial w_{kj}^{(2)}}=\frac{\partial E}{\partial a_k}\frac{\partial a_k}{\partial w_{kj}^{(2)}}$$




