キルヒホッフの法則は、起電力と多数の抵抗で構成される回路網の電流と電圧の関係を表す法則で、第1法則(電流則)と第2法則(電圧則)があります。
キルヒホッフの第1法則
第1法則は、回路網中の任意の1点に複数の導線がつながれているとき、それらの導線から出入りする電流の総和が0なるという法則です。この法則は、電流(電荷)の保存則を表しています。
導線の数を $n$、各電流を $J_k$ とすると、以下で表すことができます。但し、入ってくる電流と出て行く電流で符号を逆にとります。
$$\sum_{k=1}^nJ_k=0$$
キルヒホッフの第2法則
第2法則は、回路網中の任意の閉回路において、閉回路内の抵抗と電流の積の総和は、その閉回路内の起電力の総和に等しいとする法則です。この法則は、電位(エネルギー)の保存則を表しています。
抵抗を $R_k$、起電力を $E_k$ とすると、以下で表すことができます。但し、和は閉回路に沿って行い、電流も起電力も符号を考えて代数和をとります。
$$\sum_kR_kJ_k=\sum_kE_k$$
テブナンの定理
テブナンの定理とは、複雑な電気回路を単純な等価回路に置き換えることができるとする定理です。テブナンの定理は、キルヒホッフの法則から導くことができます。
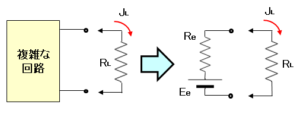
$R_L$ を接続しないときの2端子間の電圧を $E_e$ 、回路網内の全起電力をゼロ(ショート)したときの2端子間の抵抗を $R_e$ とすると、$R_L$ を流れる電流 $J_L$ は以下の式で求められます。
$$J_L=\frac{E_e}{R_e+R_L}$$
ノートンの定理
ノートンの定理とは、電圧源と抵抗で表される等価回路の代わりに、内部抵抗が無限大の電流源と抵抗で表すことができるとする定理です。
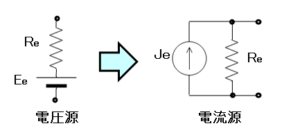
等価回路の電圧源を $E_e$ 、抵抗を $R_e$ とすると、以下の電流をもつ電流源 $J_e$ と抵抗 $R_e$ により表すことができます。
$$J_e=\frac{E_e}{R_e}$$