四端子回路
四端子回路とは、入力2端子と出力2端子を持つ回路で、簡単なフィルタ回路やトランジスタなどは四端子回路とみなすことができます。
基本行列
四端子回路の基本行列は、四端子回路の電圧と電流の関係を表した行列です。
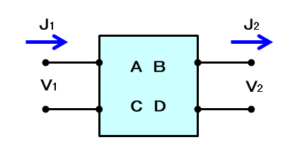
四端子回路の左側を入力(電圧:$V_1$、電流:$J_1$)、右側を出力(電圧:$V_2$、電流:$J_2$)とすると、以下の関係で表すことができます。
$$\left(\begin{array}{cc} V_1 \\ J_1 \end{array}\right)=
\left(\begin{array}{cc} A & B \\ C & D \end{array}\right)
\left(\begin{array}{cc} V_2 \\ J_2 \end{array}\right) -①$$
基本行列の各パラメタ($A$、$B$、$C$、$D$)は四端子定数と呼ばれます。
インピーダンス行列
インピーダンス行列(Z行列)とは、基本行列の代わりに、インピーダンスで表した行列です。尚、入力側と出力側を対称にするため、$J_2$ の向きを逆にしていることに注意して下さい。
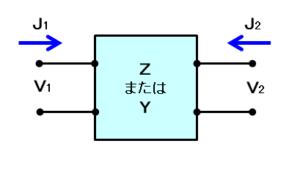
インピーダンス行列は以下で表されます。
$$\left(\begin{array}{cc} V_1 \\ V_2 \end{array}\right)=
\left(\begin{array}{cc} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{array}\right)
\left(\begin{array}{cc} J_1 \\ J_2 \end{array}\right) -②$$
アドミッタンス行列
アドミッタンス行列(Y行列)とは、基本行列の代わりに、アドミッタンスで表した行列です。
$$\left(\begin{array}{cc} J_1 \\ J_2 \end{array}\right)=
\left(\begin{array}{cc} Y_{11} & Y_{12} \\ Y_{21} & Y_{22} \end{array}\right)
\left(\begin{array}{cc} V_1 \\ V_2 \end{array}\right)$$
相反定理
相反定理とは、四端子回路の入力側と出力側の対称性を表す関係式です。相反定理は、
- 入力側に電圧 $V$ をかけて、出力側を短絡させた場合、出力側に流れる電流 $J_2$
- 出力側に電圧 $V$ をかけて、入力側を短絡させた場合、入力側に流れる電流 $J_1$
の2つのケースで、それぞれの電流は等しい($J_1=J_2=J$)ことを表します。この定理は、四端子回路が抵抗・コンデンサ・コイルなどの受動素子で構成される場合に成り立ちます。
インピーダンス行列の相反定理
インピーダンス行列の相反定理は以下で表されます。
$$Z_{12}=Z_{21} -③$$
③の導出
ケース1の場合の②は以下で表され、
$$\left(\begin{array}{cc} V \\ 0 \end{array}\right)=
\left(\begin{array}{cc} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{array}\right)
\left(\begin{array}{cc} 0 \\ J \end{array}\right)$$
ケース2の場合の②は以下で表されるため、
$$\left(\begin{array}{cc} 0 \\ V \end{array}\right)=
\left(\begin{array}{cc} Z_{11} & Z_{12} \\ Z_{21} & Z_{22} \end{array}\right)
\left(\begin{array}{cc} J \\ 0 \end{array}\right)$$
これらより以下の関係が成り立ちます。
$$\frac{V}{J}=Z_{12}=Z_{21}$$
基本行列の相反定理
基本行列の相反定理は以下で表されます。
$$AD-BC=1 -④$$
④の導出
四端子行列の基本行列を、インピーダンス行列に合わせて書き換えると以下になります。ここで、$J_2$ の符号を逆にしていることに注意して下さい。
$$\left(\begin{array}{cc} V_1 \\ V_2 \end{array}\right)=
\left(\begin{array}{cc} A/C & AD/C-B \\ 1/C & D/C \end{array}\right)
\left(\begin{array}{cc} J_1 \\ -J_2 \end{array}\right)$$
これに③を当てはめると、
$$\frac{AD}{C}-B=\frac{1}{C}$$
④が成り立つことが分かります。
四端子行列の合成
カスケード接続
カスケード接続とは、2つの四端子回路を並べたもので、合成された基本行列は以下で表されます。
$$\left(\begin{array}{cc} A’ & B’ \\ C’ & D’ \end{array}\right)
=\left(\begin{array}{cc} A_1 & B_1 \\ C_1 & D_1 \end{array}\right)\left(\begin{array}{cc} A_2 & B_2 \\ C_2 & D_2 \end{array}\right)$$




