音波の波動方程式
音波とは、気体や液体、個体などに関わらず、物質の中を伝わる疎密波(縦波)です。
物質の微小部分の変位を $\xi(x,t)$ とした場合、連続体の運動方程式は以下で表されます。尚、$\rho$ は密度、$p$ は圧力です。
$$\rho\frac{\partial v}{\partial t}=-\frac{\partial p}{\partial x} -①$$$$v=\frac{\partial\xi}{\partial t}$$
このとき、$c$ を波動の伝わる速さ(音速)とすると、音波の波動方程式は以下になります(②の導出)。
$$\frac{\partial^2p}{\partial x^2}=\frac{1}{c^2}\frac{\partial^2p}{\partial t^2} -②$$$$c=\sqrt{\frac{\kappa}{\rho}}$$
尚、$\kappa$ は体積断熱率で、圧力と体積変化の関係を表します。
$$\Delta p=-\kappa\frac{\Delta V}{V}$$
また、音速は比熱比 $\gamma$($=C_p/C_v$)を使って以下のように表すこともできます(③の導出)。
$$c=\sqrt{\frac{\gamma p}{\rho}} -③$$
②の導出
一辺が($\Delta x,1,1$)、体積が $V=\Delta x$ の微小部分を考えます。
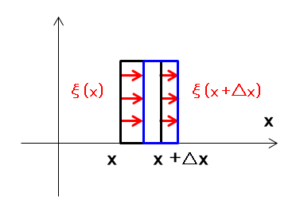
$x$ 軸方向の変位を $\xi$ とすると、$\Delta V$ は、$x$ での変位 $\xi(x)$ と $x+\Delta x$ での変位 $\xi(x+\Delta x)$ の差分に比例するため、
$$\Delta V=\xi(x+\Delta x)-\xi(x)=\frac{\partial\xi}{\partial x}\Delta x=\frac{\partial\xi}{\partial x}V$$
この微小変位を含む体積は、
$$V+\Delta V=\Big(1+\frac{\partial\xi}{\partial x}\Big)V$$$$\frac{\Delta V}{V}=\frac{\partial\xi}{\partial x}$$
これに体積弾性率は、
$$\Delta p=-\kappa\frac{\Delta V}{V} -(1)$$
であるから、これを使うと、
$$\Delta p=-\kappa\frac{\partial\xi}{\partial x}$$
この両辺を時間で2回微分して、①を使うと以下になります。
$$\frac{\partial^2p}{\partial t^2}=-\kappa\frac{\partial}{\partial x}\frac{\partial^2\xi}{\partial t^2}=\frac{\kappa}{\rho}\frac{\partial^2p}{\partial x^2}$$
③の導出
ポアソンの状態方程式より、$pV^\gamma=\alpha$(定数)。これを、$p=\alpha V^{-\gamma}$ として両辺を $V$ で微分し、
$$\frac{dp}{dV}=-\alpha\gamma V^{-\gamma-1}=-\frac{\gamma p}{V}$$
体積弾性率(1) の定義に代入すると、
$$\kappa=-\frac{\Delta p}{\Delta V/V}=\gamma p$$
これを②の音速に代入すると③が得られます。
音のエネルギー
波動方程式②の正弦波の解を以下で置くと、
$$p(x,t)=A\sin{k(x-ct)}$$
①に代入して積分すると、変位は以下になります。
$$\xi=\xi_0\cos{k(x-ct)}$$$$\xi_0\equiv\frac{A}{\rho c^2k}$$
波動のエネルギーは、周波数と振幅の2乗に比例するため、音のエネルギーは以下で表されます。
$$I=\frac{\rho\omega^2\xi_0^2c}{2}=\frac{A^2}{2\rho c}$$




