スネルの法則とは
スネルの法則とは、2つの媒質が接する境界面を横切る光線(光)に関する法則で、反射の法則と屈折の法則から構成されます。
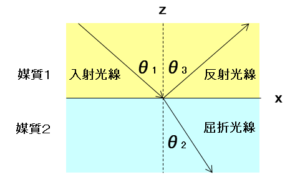
ここで、入射光線、反射光線、屈折光線がそれぞれ入射面の法線となす各を、入射角 $\theta_1$ 、屈折角 $\theta_2$ 、反射角 $\theta_3$ と呼び、下図のように定義します。
反射の法則
反射の法則とは、入射角 $\theta_1$ と反射角 $\theta_3$ が等しいとする法則です。
$$\theta_1=\theta_3 -①$$
屈折の法則
屈折の法則とは、入射角 $\theta_1$ と屈折角 $\theta_2$ の関係を表す法則です。次の式を満足する $n_{12}$ は、2つの媒質の屈折率の組合せによって決まる定数(相対屈折率)で、入射角に依らないことが知られています。
$$\frac{\sin{\theta_1}}{\sin{\theta_2}}=n_{12} -②$$
屈折率
屈折率には、絶対屈折率と相対屈折率の2つがあります。
絶対屈折率
絶対屈折率とは、真空に対する屈折率で、単に屈折率と言えばこの絶対屈折率を指します。絶対屈折率は、光速と媒質内の伝播速度の比として定義されます。媒質1内の伝播速度を $v_1$ とすると、媒質1の絶対屈折率 $n_1$ は以下で表されます。
$$n_1\equiv\frac{c}{v_1} -③$$
媒質1が空気の場合、空気の絶対屈折率は $n_a\cong1.00029$ となります。この空気の絶対屈折率が誤差範囲とみなせる場合は、空気中での媒質の相対屈折率を絶対屈折率として扱うことが可能です。
相対屈折率
相対屈折率とは、2つの媒質の境界面での屈折率です。媒質1での伝播速度を $v_1$ 、媒質2での伝播速度を $v_2$ とすると、相対屈折率 $n_{12}$ は以下で表されます。
$$n_{12}=\frac{v_1}{v_2} -④$$
この相対屈折率は、③より絶対屈折率の比で表すことができます。
$$n_{12}=\frac{n_2}{n_1}$$
さらに、媒質1→媒質2の相対屈折率を $n_{12}$ 、媒質2→媒質3の相対屈折率を $n_{23}$ とすると、媒質1→媒質3の相対屈折率 $n_{13}$ は以下で表されることが分かります。
$$n_{13}=\frac{n_3}{n_1}=n_{12}n_{23}$$
スネルの法則を導く
媒質1の入力光線を電場 ${\bf E}_1$ 、媒質2の屈折光線を電場 ${\bf E}_2$ 、反射光線を電場 ${\bf E}_3$ とすると、これらはマクスウェル方程式より波動として表すことができます。尚、$(\alpha_i,\beta_i,\gamma_i)$ は各 $(x,y,z)$ 軸に対する方向余弦、$v_i$ は媒質内の伝播速度、$\delta_i$ は位相を表します。
$${\bf E}_1={\bf E}_{10}\sin{\left(\omega_1\Big(t-\frac{\alpha_1x+\beta_1y+\gamma_1z}{v_1}\Big)+\delta_1\right)}$$$${\bf E}_2={\bf E}_{20}\sin{\left(\omega_2\Big(t-\frac{\alpha_2x+\beta_2y+\gamma_2z}{v_2}\Big)+\delta_2\right)}$$$${\bf E}_3={\bf E}_{30}\sin{\left(\omega_3\Big(t-\frac{\alpha_3x+\beta_3y+\gamma_3z}{v_1}\Big)+\delta_3\right)}$$
ここで、入力光線が $xz$-平面上($\beta_1=0$)にあることと、位相 $\delta_1=0$ を仮定しても一般性は失われません。さらに、境界条件として、媒質間の電場の接線成分が境界面の両側で等しくなるため、
$$E_{1x}+E_{3x}=E_{2x}$$$$E_{1y}+E_{3y}=E_{2y}$$
これが成り立つためには、${\bf E}_i$ の $\sin$ の中が等しくなる必要があります。従って、
$$\omega_1=\omega_2=\omega_3$$$$\beta_2=\beta_3=0$$$$\delta_2=\delta_3=0$$
これらより、
$$\frac{\alpha_1}{v_1}=\frac{\alpha_2}{v_2}=\frac{\alpha_3}{v_1}$$
左辺と右辺より、$\alpha_1=\alpha_3$ より $\cos{\theta_1}=\cos{\theta_3}$ であるため、反射の法則①が導かれます。また、方向余弦 $\alpha_1$ と $\alpha_2$ について、入射角 $\theta_1$ と屈折角 $\theta_2$ で表すと、
$$\alpha_1=\cos{\Big(\frac{\pi}{2}-\theta_1\Big)}=\sin{\theta_1}$$$$\alpha_2=\cos{\Big(\frac{\pi}{2}-\theta_2\Big)}=\sin{\theta_2}$$
左辺と中辺より、
$$\frac{\sin{\theta_1}}{v_1}=\frac{\sin{\theta_2}}{v_2}$$
これと④より、屈折の法則②が導かれます。
$$\frac{\sin{\theta_1}}{\sin{\theta_2}}=\frac{v_1}{v_2}=n_{12}$$




