位数計算
位数計算とは、互いに素の $x$ と $m$（$x\lt m$）が与えられたとき、
$$x^r\bmod{m}=1 -①$$
を満たす最小の $r$（位数）を求める計算です。従来のコンピュータでは、位数を求める計算は計算量的に難しい問題とされていますが、量子コンピュータを利用することで高速に（実用的に）計算することができます。
尚、位相計算は因数分解の計算で利用されます。
量子アルゴリズム
量子アルゴリズムでは位数計算を、次で定義されるユニタリ演算子（③の導出）と、
$$U\ket{y}\equiv\ket{xy\bmod{m}} -②$$$$U\ket{x^j\bmod{m}}=\ket{x^{j+1}\bmod{m}} -③$$
その固有関数
$$\ket{\phi_l}=\frac{1}{\sqrt{r}}\sum_{j=0}^{r-1}e^{-2\pi ijl/r}\ket{x^j\bmod{m}} -④$$
および固有値 $e^{2\pi il/r}$ において、以下の量子位相推定を解く問題に置き換えることができます。（⑤の導出）
$$U\ket{\phi_l}=e^{2\pi il/r}\ket{\phi_l} -⑤$$
尚、⑤を導く際に①から得られる以下の関係式を利用しています。
$$\ket{x^r\bmod{m}}=1=\ket{1\bmod{m}}=\ket{x^0\bmod{m}} -⑥$$
⑥の関係があるため、④の右辺は位数 $r$ 個の和となり、⑤の式を得ることができます。そして、⑤の $l/r$ は量子位相推定で求めることができるので、これから①の位数 $r$ を推定することができます。
量子回路
量子位相推定では、⑤の $l/r$ を以下の量子回路を使って求めます。
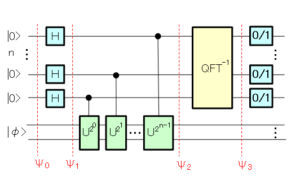
量子位相推定で見たように、アダマールゲートとユニタリゲートを通過した後の状態 $\Psi_2$ は以下になります。
$$\Psi_2=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes U^k\ket{\phi}$$
但し、下部のレジスタの $\phi$ は④で定義されており、位数 $r$ が分からないと得られないため、
$$\frac{1}{\sqrt{r}}\sum_{l=0}^{r-1}\ket{\phi_l}=\ket{1} -⑦$$
であることを利用し（⑦の導出）、$\ket{\phi_l}\to\ket{1}$ と置き換えます。
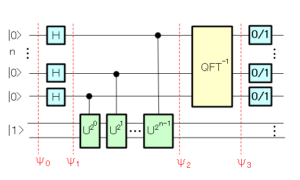従って、
$$\Psi_2=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes U^k\ket{1} -⑧$$
これを変形し、$2^nl/r=l’/r$ と置くと以下が得られます。（⑨の導出）
$$\Psi_2=\frac{1}{\sqrt{r}}\sum_{l=0}^{r-1}\Big(\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{2\pi ik(l’/r)/2^n}\ket{k}\Big)\otimes\ket{\phi_l} -⑨$$
括弧の中について $l=0$ から $r-1$ までの重ね合わせ状態となっていますが、下部のレジスタを測定することにより、上部のレジスタについても一つの状態 $\Psi_2’$ に確定します。
$$\Psi_2’=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{2\pi ik(l’/r)/2^n}\ket{k}$$
量子フーリエ変換は以下で表されるため、右辺で $j\to l’/r$ のように置き換えると、逆量子フーリエ変換 $\mathrm{QFT^{-1}}$ を行うことにより、$l’/r$ が得られることが分かります。
$$\ket{j} \to \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{2\pi ikj/N}\ket{k}$$
導出
③を導く
$p$ と $q$ を自然数として、$x^j=pm+q$ と置くと、③の両辺は、
$$U\ket{x^j\bmod{m}}=U\ket{q}=\ket{xq\bmod{m}}$$$$\ket{x^{j+1}\bmod{m}}=\ket{x(pm+q)\bmod{m}}=\ket{xq\bmod{m}}$$
これより③が成り立つことが分かります。
⑤を導く
④にユニタリ演算子を作用させ、③を使うと、
$$U\ket{\phi_l}=\frac{1}{\sqrt{r}}\sum_{j=0}^{r-1}e^{-2\pi ijl/r}U\ket{x^j\bmod{m}}$$$$=\frac{1}{\sqrt{r}}\sum_{j=0}^{r-1}e^{-2\pi ijl/r}\ket{x^{j+1}\bmod{m}}$$
$$=\frac{1}{\sqrt{r}}\Big(e^{-2\pi i\cdot0\cdot l/r}\ket{x^1\bmod{m}}+\cdots$$$$+e^{-2\pi i(r-2)l/r}\ket{x^{r-1}\bmod{m}}+e^{-2\pi i(r-1)l/r}\ket{x^r\bmod{m}}\Big)$$
$$=e^{2\pi il/r}\frac{1}{\sqrt{r}}\Big(e^{-2\pi i\cdot1\cdot l/r}\ket{x^1\bmod{m}}+\cdots$$$$+e^{-2\pi i(r-1)l/r}\ket{x^{r-1}\bmod{m}}+e^{-2\pi irl/r}\ket{x^r\bmod{m}}\Big)$$
最後の項について、$e^{-2\pi il}=1$ より $e^{-2\pi irl/r}=e^{-2\pi i\cdot0\cdot l/r}$ と書き換え、⑥を使うと、以下のように書くことができます。
$$=e^{2\pi il/r}\frac{1}{\sqrt{r}}\Big(e^{-2\pi i\cdot1\cdot l/r}\ket{x^1\bmod{m}}+\cdots$$$$+e^{-2\pi ij(r-1)/r}\ket{x^{r-1}\bmod{m}}+e^{-2\pi i\cdot0\cdot l/r}\ket{x^0\bmod{m}}\Big)$$$$=e^{2\pi il/r}\frac{1}{\sqrt{r}}\sum_{j=0}^{r-1}e^{-2\pi ijl/r}\ket{x^j\bmod{m}}$$$$=e^{2\pi il/r}\ket{\phi_l}$$
最後は④を代入することで⑤が成り立つことが導かれます。
⑦を導く
⑦の左辺に④を代入すると、
$$\frac{1}{\sqrt{r}}\sum_{l=0}^{r-1}\ket{\phi_l}=\frac{1}{r}\sum_{j=0}^{r-1}\Big(\sum_{l=0}^{r-1}e^{-2\pi ijl/r}\Big)\ket{x^j\bmod{m}}$$
$j\ne0$ の場合、この括弧の中は、$r$ 等分割された単位円上の点の座標を足し合わせる問題となり、常に０となります。$j\ge2$ の場合でも、単位円上の点の数と位置は変わりません。
$$\sum_{l=0}^{r-1}e^{-2\pi ijl/r}=\sum_{l=0}^{r-1}(e^{-2\pi il/r})^j=0$$
$j=0$ の場合、
$$\frac{1}{\sqrt{r}}\sum_{l=0}^{r-1}\ket{\phi_l}=\frac{1}{r}\sum_{l=0}^{r-1}e^{-2\pi i\cdot0\cdot l/r}\ket{x^0\bmod{m}}$$$$=\ket{1}$$
⑨を導く
⑧に⑦を代入し、⑤を使うと、
$$\Psi_2=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes U^k\frac{1}{\sqrt{r}}\sum_{l=0}^{r-1}\ket{\phi_l}$$$$=\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\ket{k}\otimes\frac{1}{\sqrt{r}}\sum_{l=0}^{r-1}e^{2\pi ikl/r}\ket{\phi_l}$$$$=\frac{1}{\sqrt{r}}\sum_{l=0}^{r-1}\Big(\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}e^{2\pi ikl/r}\ket{k}\Big)\otimes\ket{\phi_l}$$
$0\le l/r\lt 1$ であるため $2^nl/r=l’/r$ と置くと⑨が得られます。
