部分ゲーム
部分ゲームとは、展開型ゲームの部分木について、全ての情報集合がその部分木以外の情報集合を含まない場合です。尚、情報集合とは、行動決定においてプレイヤが知っている情報の状態(選択肢の範囲)を表します。
次のような展開型ゲームの2人のプレイヤ $A$ 、$B$ の行動決定($X,Y$)において、同時に行う場合を左図、逐次($A\to B$ の順)で行う場合を右図に表します。括弧の数字はそれぞれ $A,B$ の利得とします。
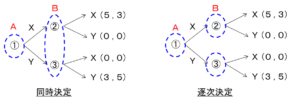
図中の点線は情報集合を表します。同時決定の場合は、$B$ は $A$ の決定の結果を知らないで行動決定しますが、逐次決定の場合は、$B$ は $A$ の決定の結果を知った上で行動決定を行います。
従って、逐次決定の場合の $B$ は、 ②は③と独立して行動決定することができ、③は②と独立して行動決定ができます。一方、同次決定の場合の②と③は独立して行動決定することはできません。
以上より、逐次決定の場合の②と③を起点とする展開ゲームは、①を起点する展開ゲームの部分ゲームとなります。
部分ゲーム完全均衡
部分ゲーム完全均衡とは、元の展開ゲームの全ての部分ゲームに対して、ナッシュ均衡を与える行動戦略の組を指します。上の例における同時決定の利得表配下で、
| $A\backslash B$ | $B:X$ | $B:Y$ |
| $A:X$ | $(5,3)$ | $(0,0)$ |
| $A:Y$ | $(0,0)$ | $(3,5)$ |
逐次決定の利得表は以下で表されます。尚、「$B:Y/X$」という表記は、$A$ が $X$ の行動決定(”$/$”の左側)を行えば $B$ は $Y$、$A$ が $Y$ の行動決定(”$/$”の右側)を行えば $B$ は $X$ の行動決定を行うという戦略を表します。
| $A\backslash B$ | $B:X/X$ | $B:X/Y$ | $B:Y/X$ | $B:Y/Y$ |
| $A:X$ | $(\underline{5}, \underline{3})$ | $(\underline{5}, \underline{3})$ | $(0,0)$ | $(0,0)$ |
| $A:Y$ | $(0,0)$ | $(3,\underline{5})$ | $(0,0)$ | $(\underline{3}, \underline{5})$ |
ナッシュ均衡になる戦略
ナッシュ均衡に下線を付けました。展開ゲーム全体を見ると($A:X,B:X/X$)、($A:X,B:X/Y$)、($A:Y,B:Y/Y$)がナッシュ均衡となります。
例えば($A:X,B:X/Y$)は、以下ようにナッシュ均衡になっているとが分かります。
| $A\backslash B$ | $B:X/Y$ |
| $A:X$ | $(\underline{5}, \underline{3})$ |
| $A:Y$ | $(3,\underline{5})$ |
一方($A:Y,B:X/Y$)は、ナッシュ均衡にはなっていません。
部分ゲーム完全均衡になる戦略
全ての部分ゲームでナッシュ均衡(部分ゲーム完全均衡)となるのは($A:X,B:X/Y$)のみです。
例えば($A:X,B:X/X$)は、②を始点とする部分ゲーム($A:X$)ではナッシュ均衡ですが、③を始点とする部分ゲーム($A:Y$)ではナッシュ均衡ではありません。
また($A:Y,B:Y/Y$)は、③を始点とする部分ゲーム($A:Y$)ではナッシュ均衡ですが、②を始点とする部分ゲーム($A:X$)ではナッシュ均衡ではありません。
| ② $A:X$ |
$B:X/X$ | $B:X/Y$ | $B:Y/X$ | $B:Y/Y$ |
| $\underline{3}$ | $\underline{3}$ | $0$ | $0$ |
| ③ $A:Y$ |
$B:X/X$ | $B:X/Y$ | $B:Y/X$ | $B:Y/Y$ |
| $0$ | $\underline{5}$ | $0$ | $\underline{5}$ |
一方($A:X,B:X/Y$)は、②を始点とする部分ゲームおよび③を始点とする部分ゲームの両方でナッシュ均衡となります。




