ラザフォード散乱
ラザフォード散乱とは、クーロン力による同符号の過電粒子間の弾性散乱です。ラザフォード散乱により、原子内のプラスの電荷の分布が一様に広がったものではなく、原子の中心(原子核)に収集していることが証明されました。
ラザフォード散乱の軌道
ラザフォード散乱の軌道をニュートンの運動方程式から導きます。まず、中心力でのニュートンの運動方程式($r$ 成分)は以下になります。
$$F_r=mA_r=m(\ddot{r}-r\dot{\theta}^2)$$
入射粒子と散乱中心(原子核)の電荷を$q$ と $Q$ とすると、クーロン力は以下で表され、
$$F_r=\frac{qQ}{4\pi\epsilon_0r^2}\equiv\frac{K}{r^2}$$
これを $r$ 方向の運動方程式に代入すると以下になります。ここで、$l=mr^2\dot{\theta}$ で角運動量を表します。
$$\frac{d^2r}{dt^2}-\frac{K}{mr^2}-\frac{l^2}{m^2r^3}=0 -①$$
運動方程式を解くと以下の解が得られます。この式の導出はこの記事の最後で行います。
$$r=\frac{\lambda}{\epsilon\sin{(\theta+\alpha)}-1} -②$$
$$\lambda\equiv\frac{l^2}{mK} , \epsilon\equiv\frac{Cl^2}{mK}$$
衝突係数
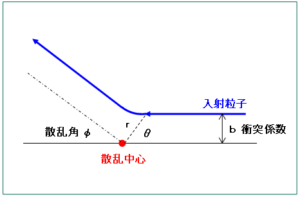
衝突係数とは、入射粒子の入射方向と散乱中心とのずれを表します。入射粒子の初速度を $v_0$ とすると、角運動量は衝突係数により以下で表されます。尚、$\sin{\theta}=b/r$ としています。
$$l=mrv_0\sin{\theta}=mv_0b -③$$
微分散乱断面積
微分散乱断面積とは、入射粒子からみて単位面積当たり1個の散乱中心がある場合に、これによって散乱されて、散乱角の単位立体角に出ていく粒子の割合です。
衝突係数 $b\sim b+db$ の入射粒子が散乱角 $\phi\sim\phi+d\phi$ から出ていくと仮定し、単位面積の入射粒子と散乱中心の個数を $N$ と $n$ とするとき、散乱中心から距離 $R$ 、断面積 $\Delta S$ の検出器に飛び込む散乱粒子の数 $N’$ は以下で表されます。
$$N’=Nn\cdot 2\pi b|db|\cdot\frac{\Delta S}{2\pi R\sin{\phi}\cdot Rd\phi} -④$$
ここで、$2\pi b|db|$ は、単位面積当たり1個の散乱中心が存在する場合の $b\sim b+db$ の面積の割合、$2\pi R\sin{\phi}\cdot Rd\phi$ は散乱中心から距離 $R$ にある幅 $d\phi$ の円環の面積です。
このとき、微分散乱断面積 $\sigma$ を以下で定義すると、
$$N’=Nn\sigma(\phi)\frac{\Delta S}{R^2}$$
下記のように表すことができます。
$$\sigma(\phi)\equiv\frac{b}{\sin{\phi}}\Big|\frac{db}{d\phi}\Big|=\frac{K^2}{4m^2v_0^4\sin^4{(\phi/2)}} -⑤$$
ここで、$\phi$ は散乱角、$v_0$ と $m$ は入射粒子の初速度と質量です。
導出
②を導く
①から②の導出を行います。まず、①で時間微分を $\theta$ の微分に置換えます。$\dot{\theta}=l/mr^2$ であることから、
$$\frac{d}{dt}=\frac{d\theta}{dt}\frac{d}{d\theta}=\frac{l}{mr^2}\frac{d}{d\theta}$$
であるため、以下のように置き換えられます。
$$\frac{d^2r}{dt^2}=\frac{l^2}{m^2r^2}\frac{d}{d\theta}\left(\frac{1}{r^2}\frac{dr}{d\theta}\right)$$
次に $u=1/r$ と置くと、
$$\frac{1}{r^2}\frac{dr}{d\theta}=-\frac{du}{d\theta}$$
となるため、以下のように書き換えられます。
$$\frac{d^2r}{dt^2}=-\frac{l^2u^2}{m^2}\frac{d^2u}{d\theta^2}$$
これを①に代入すると、以下になります。
$$\frac{d^2u}{d\theta^2}=-u-\frac{mK}{l^2}$$
この微分方程式の解が以下であることは、実際に代入してみると分かります。ここで $C$ と $\alpha$ は積分定数です。
$$u=C\sin{(\theta+\alpha)}-\frac{mK}{l^2}$$
最後に、$r=1/u$ とすると②になります。
⑤を導く
以下、3つの境界条件を考えます。
- $t\to-\infty$ のとき、$\theta=0$ 、$r\to\infty$
- $t\to-\infty$ のとき、$\theta=0$ 、$\dot{r}=-v_0$
- $t\to\infty$ のとき、$\theta=\pi-\phi$ 、$r\to\infty$
条件1を②に適用すると以下になります。
$$\epsilon\sin{\alpha}=1 -(1)$$
次に条件2のために以下を求めます。③と$l=mr^2\dot{\theta}$を使い、②の微分を代入すると、
$$\frac{dr}{dt}=\dot{\theta}\frac{dr}{d\theta}=\frac{bv_0}{r^2}\frac{dr}{d\theta}$$$$=-\frac{bv_0}{\lambda}\epsilon\cos{(\theta+\alpha)}$$
これに初期条件2を適用し、②と③を使って $\lambda$ と $l$ を消去すると、
$$\epsilon\cos{\alpha}=\frac{\lambda}{b}=\frac{bmv_0^2}{K} -(2)$$
条件3を①に適用すると以下になります。
$$\epsilon\sin{(\pi-\phi+\alpha)}=\epsilon\sin{(\phi-\alpha)}=1$$
これと (1) より、
$$\sin{(\phi-\alpha)}=\sin{\alpha}$$
であるから、$\phi=2\alpha$ であることが分かります。これと、(1) と (2) より、
$$\tan{\alpha}=\tan{\frac{\phi}{2}}=\frac{K}{bmv_0^2}$$$$b=\frac{K}{mv_0^2}\tan^{-1}{\frac{\phi}{2}} -(3)$$
このとき、
$$\frac{db}{b\phi}=\frac{-K}{2mv_0^2\sin^2{(\phi/2)}} -(4)$$
(3)、(4)を⑤の左辺に代入し、関係式 $\sin{\phi}=2\sin{(\phi/2)}\cos{(\phi/2)}$ を使うと⑤が得られます。
$$\frac{b}{\sin{\phi}}\Big|\frac{db}{d\phi}\Big|=\frac{K^2\cos{(\phi/2)}}{2m^2v_0^4\sin{\phi}\sin^3{(\phi/2)}}$$$$=\frac{K^2}{4m^2v_0^4\sin^4{(\phi/2)}}$$




