クローニッヒ・ペニー・モデル
クローニッヒ・ペニー・モデルとは、結晶内での電子の挙動の近似的なモデルで、周期的な1次元の井戸型ポテンシャルとして表されます。このモデルにより、結晶内の電子がエネルギーバンドを持つことが導かれます。
1次元の井戸型ポテンシャルは、以下のように、周期が $a+b$ で、$x=0\sim a$ では $V(x)=0$ 、$x=-b\sim 0$ では $V(x)=V_0$ の値を持ちます。
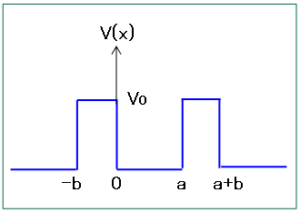
1次元のシュレディンガーの波動方程式は以下になります。
$$-\frac{\hbar^2}{2m}\frac{d^2\phi}{dx^2}+V(x)=\epsilon\phi$$
固有関数
一般に波動方程式の解は左右に進行する波の1次結合で表されるため、$0\le x\le a$ における固有関数とエネルギー固有値は、
$$\phi_1(x)=Ae^{i\alpha x}+Be^{-i\alpha x} -①$$$$\epsilon=\frac{\hbar^2\alpha^2}{2m}$$
$-b\le x\le 0$ における固有関数とエネルギー固有値は、
$$\phi_2(x)=Ce^{i\beta x}+De^{-i\beta x} -②$$$$\epsilon=\frac{\hbar^2\beta^2}{2m}+V_0$$
境界条件
境界において固有関数は連続であるため、以下の境界条件を設定します。つまり、$x=0$ において、
- 固有関数①と②は等しい。
$$\phi_1(0)=\phi_2(0) -③$$ - 固有関数①と②の微分は等しい。
$$\frac{\partial\phi_1}{\partial x}(0)=\frac{\partial\phi_2}{\partial x}(0) -④$$
一方、以下のブロッホの定理
$$\phi({\bf r}+{\bf R})=\phi({\bf r})e^{i{\bf k}\cdot{\bf R}}$$
が、$x=a$ と $x=-b$ において、
- 固有関数①と②で成り立つ。
$$\phi_1(a)=\phi_2(-b)e^{ik(a+b)} -⑤$$ - 固有関数①と②の微分で成り立つ。
$$\frac{\partial\phi_1}{\partial x}(a)=\frac{\partial\phi_2}{\partial x}(-b)e^{ik(a+b)} -⑥$$
バンドギャップ
周期条件③~⑥により、波動ベクトル $k$ の条件は以下になります。
$$\cos{k(a+b)}=-\frac{\alpha^2+\beta^2}{2\alpha\beta}\sin{\alpha a}\sin{\beta b}+\cos{\alpha a}\cos{\beta b} -⑦$$
ここで、$b\to 0$ の極限を取ると $\alpha^2\ll \beta^2$ 、$\sin{\beta b}\cong\beta b$ 、$\cos{\beta b}\cong 1$ であるから、
$$\cos{ka}=-\frac{\beta^2b}{2\alpha}\sin{\alpha a}+\cos{\alpha a} -⑧$$
左辺は $-1\le\cos{ka}\le 1$ であるため、その範囲を取る $\alpha$ 、$\beta$(固有エネルギー $\epsilon$)の値が許されます。
⑦を導く
①と②をそれぞれ境界条件③、④、⑤、⑥に代入すると、
$$A+B=C+D -(1)$$$$\alpha A-\alpha B=\beta C-\beta D -(2)$$$$Ae^{i\alpha a}+Be^{-i\alpha a}=\Big(Ce^{-i\beta b}+De^{i\beta b}\Big)e^{ik(a+b)} -(3)$$$$\alpha Ae^{i\alpha a}-\alpha Be^{-i\alpha a}=\Big(\beta Ce^{-i\beta b}-\beta De^{i\beta b}\Big)e^{ik(a+b)} -(4)$$
これらの方程式をまとめると、
$$\left(\begin{array}{ccc} 1 & 1 & -1 & -1 \\
\alpha & -\alpha & -\beta & \beta \\
e^{i\alpha a} & e^{-i\alpha a} & -e^{-i\beta b}e^{ik(a+b)} & -e^{i\beta b}e^{ik(a+b)} \\
\alpha e^{i\alpha a} & -\alpha e^{-i\alpha a} & -\beta e^{-i\beta b}e^{ik(a+b)} & \beta e^{i\beta b}e^{ik(a+b)} \end{array}\right)
\left(\begin{array}{ccc} A \\ B \\ C \\ D \end{array}\right)=0$$
この方程式が自明な解($A=B=C=D=0$)以外の解を持つ条件は、左辺の行列式が0になることです。
$$\left|\begin{array}{ccc} 1 & 1 & -1 & -1 \\
\alpha & -\alpha & -\beta & \beta \\
e^{i\alpha a} & e^{-i\alpha a} & -e^{-i\beta b}e^{ik(a+b)} & -e^{i\beta b}e^{ik(a+b)} \\
\alpha e^{i\alpha a} & -\alpha e^{-i\alpha a} & -\beta e^{-i\beta b}e^{ik(a+b)} & \beta e^{i\beta b}e^{ik(a+b)} \end{array}\right|
=0$$
一般に、4×4の行列 $M$ の行列式 $|M|$ は、行列 $M$ から $i$ 行と $j$ 列を除いた行列の行列式 $|M_{ij}|$(余因子)により、以下で表されます。尚、$m_{ij}$ は行列 $M$ の要素です。
$$|M|=m_{11}|M_{11}|-m_{12}|M_{12}|+m_{13}|M_{13}|-m_{14}|M_{14}|$$
右辺を各項に分けて計算すると、
$$\mbox{第1項}=|M_{11}|=\left|\begin{array}{ccc} -\alpha & -\beta & \beta \\
e^{-i\alpha a} & -e^{-i\beta b}e^{ik(a+b)} & -e^{i\beta b}e^{ik(a+b)} \\
-\alpha e^{-i\alpha a} & -\beta e^{-i\beta b}e^{ik(a+b)} & \beta e^{i\beta b}e^{ik(a+b)} \end{array}\right|$$$$=2\alpha\beta e^{2ik(a+b)}+\beta^2e^{-i\alpha a}(e^{i\beta b}-e^{-i\beta b})e^{ik(a+b)}-\alpha\beta e^{-i\alpha a}(e^{i\beta b}+e^{-i\beta b})e^{ik(a+b)}$$
$$\mbox{第2項}=-|M_{12}|=-\left|\begin{array}{ccc} \alpha & -\beta & \beta \\
e^{i\alpha a} & -e^{-i\beta b}e^{ik(a+b)} & -e^{i\beta b}e^{ik(a+b)} \\
\alpha e^{i\alpha a} & -\beta e^{-i\beta b}e^{ik(a+b)} & \beta e^{i\beta b}e^{ik(a+b)} \end{array}\right|$$$$=2\alpha\beta e^{2ik(a+b)}-\beta^2e^{i\alpha a}(e^{i\beta b}-e^{-i\beta b})e^{ik(a+b)}-\alpha\beta e^{i\alpha a}(e^{i\beta b}+e^{-i\beta b})e^{ik(a+b)}$$
$$\mbox{第3項}=-|M_{13}|=-\left|\begin{array}{ccc}\alpha & -\alpha & \beta \\
e^{i\alpha a} & e^{-i\alpha a} & -e^{i\beta b}e^{ik(a+b)} \\
\alpha e^{i\alpha a} & -\alpha e^{-i\alpha a} & \beta e^{i\beta b}e^{ik(a+b)} \end{array}\right|$$$$=2\alpha\beta-\alpha^2(e^{i\alpha a}-e^{-i\alpha a})e^{i\beta b}e^{ik(a+b)}-\alpha\beta(e^{i\alpha a}+e^{-i\alpha a})e^{i\beta b}e^{ik(a+b)}$$
$$\mbox{第4項}=|M_{14}|=\left|\begin{array}{ccc} \alpha & -\alpha & -\beta \\
e^{i\alpha a} & e^{-i\alpha a} & -e^{-i\beta b}e^{ik(a+b)} \\
\alpha e^{i\alpha a} & -\alpha e^{-i\alpha a} & -\beta e^{-i\beta b}e^{ik(a+b)} \end{array}\right|$$$$=2\alpha\beta+\alpha^2(e^{i\alpha a}-e^{-i\alpha a})e^{-i\beta b}e^{ik(a+b)}-\alpha\beta(e^{i\alpha a}+e^{-i\alpha a})e^{-i\beta b}e^{ik(a+b)}$$
これらの項を合計すると、
$$|M|=4\alpha\beta(1+e^{2ik(a+b)})-(\alpha^2+\beta^2)(e^{i\alpha a}-e^{-i\alpha a})(e^{i\beta b}-e^{-i\beta b})e^{ik(a+b)}$$$$-2\alpha\beta(e^{i\alpha a}+e^{-i\alpha a})(e^{i\beta b}+e^{-i\beta b})e^{ik(a+b)}$$$$=4\alpha\beta(1+e^{2ik(a+b)})+4(\alpha^2+\beta^2)e^{ik(a+b)}\sin{\alpha a}\sin{\beta b}$$$$-8\alpha\beta e^{ik(a+b)}\cos{\alpha a}\cos{\beta b}$$
この行列式を0と置き、両辺を $8\alpha\beta e^{ik(a+b)}$ で割ると、
$$\frac{e^{-ik(a+b)}+e^{ik(a+b)}}{2}=-\frac{\alpha^2+\beta^2}{2\alpha\beta}\sin{\alpha a}\sin{\beta b}+\cos{\alpha a}\cos{\beta b}$$
左辺は余弦関数で書き換えられるため⑦が得られます。




