伝達関数とは

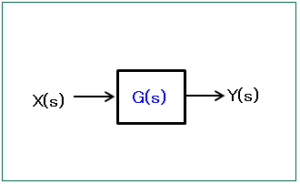
伝達関数とは、出力信号のラプラス変換 $Y(s)$ と出力信号のラプラス変換 $X(s)$ の比で表されます。伝達関数により、安定性などの制御システムの特性を解析することができます。

一般に入力信号を $x(t)$ 、出力信号を $y(t)$ とすると、多くのシステムは以下の線形微分方程式で表すことができます。

$$a_ny^{(n)}(t)+\cdots+a_1\dot{y}(t)+a_0y(t)=b_mx^{(m)}(t)+\cdots+b_1\dot{x}(t)+b_0x(t)　　-①$$

これにラプラス変換を施し、初期値が全て０であるとき、$X(s)={\mathcal L}[x(t)]$ と $Y(s)={\mathcal L}[y(t)]$ の関係式は、

$$(a_ns^n+\cdots+a_1s+a_0)Y(s)=(b_ms^m+\cdots+b_1s+b_0)X(s)$$

となります。これにより伝達関数 $G(s)$ は以下で定義されます。

$$G(s)\equiv\frac{Y(s)}{X(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_0}{a_ns^n+a_{n-1}s^{n-1}+\cdots+a_0}　　-②$$

伝達関数の分母を０にする $n$ 個の解を $p_i$ 、分子を０とする $m$ 個の解を $q_j$ とすると以下のように書き換えられます。尚、ここで $n\ge m$ です。

$$G(s)=K\frac{(s-q_1)(s-q_2)\cdots(s-q_m)}{(s-p_1)(s-p_2)\cdots(s-p_n)}　　-③$$

伝達関数の標準形

制御工学では、電気系・機械系・熱系などの物理学的な観点からではなく、以下の標準的な形式で記述される動的システムとして考えます。

１次遅れ要素の標準形は以下で表されます。遅れとは、入力波よりも出力波の位相が遅れていることを意味します。

$$G(s)=\frac{K}{1+Ts}　　　(T\gt0)$$

$T$ は時定数と呼ばれ、反応の速さに関するパラメタで、$K$ は定常特性と呼ばれ、十分時間が経過した後のシステムの振る舞いに関するパラメタです。

２次遅れ要素の標準形は以下で表されます。

$$G(s)=\frac{K}{(1+T_1s)(1+T_2s)}　　　(T_1,T_2\gt0)$$$$=\frac{P\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}　　　(\eta,\omega_n\gt0)$$

$\zeta$ は減衰係数と呼ばれる安定度に関するパラメタ、$\omega_n$ は固有角周波数と呼ばれる速応性に関するパラメタ、$P$ はゲインと呼ばれる定常特性に関するパラメタです。

むだ時間要素の標準形は以下で表されます。

$$G(s)=e^{-sT}　　　(T\gt0)$$

ここで $T$ はむだ時間と呼ばれます。

システムが安定であるためには、$t\to\infty$ で伝達関数 $G$ が一定値に収束する必要があります。これを言い換えると、伝搬関数の極の実部が全て負になることであることです。これは以下のことから分かります。

①で $x(t)=1$ の場合を考えると、ラプラス変換は ${\mathcal L}[1]=1/s$ であるから、③を書き換えると、

$$Y(s)=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_0}{s(s-p_1)(s-p_2)\cdots(s-p_n)}$$

この式の極 $p_j$ が $n_1$ 個の実数 $\gamma_k$ と $n_2$ 個の複素数 $\alpha_l\pm i\beta_l$ を持つとすると（$m\le n=n_1+2n_2$）、

$$Y(s)=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_0}{s(s-\gamma_1)\cdots(s-\gamma_{n1})[(s-\alpha_1)^2+\beta_1^2]\cdots[(s-\alpha_{n2})^2+\beta_{n2}^2]}$$

これを $A_k$ 、$B_l$ 、$C_l$ を定数として部分分数分解すると以下になります。

$$Y(s)=\frac{A_0}{s}+\sum_{k=1}^{n_1}\frac{A_k}{s-\gamma_k}+\sum_{l=1}^{n_2}\frac{B_l(s-\alpha_l)+C_l\beta_l}{(s-\alpha_l)^2+\beta_l^2}　　-④$$

これを逆ラプラス変換すると、

$$y(t)=A_0+\sum_{k=1}^{n_1}A_ke^{\gamma_kt}+\sum_{l=1}^{n_2}\Big(B_le^{\alpha_lt}\cos{\beta_lt}+C_le^{\alpha_lt}\sin{\beta_lt}\Big)　　-⑤$$

これより $n_1$ 個の実数 $\gamma_k$ と $n_2$ 個の実部 $\alpha_l$ が全て負であれば、$y(t)$ は以下のように収束することが分かります。

$$\lim_{t\to\infty}y(t)=A_0$$

尚、④→⑤については、次の逆ラプラス変換を使っています。

$${\mathcal L}^{-1}\Big[\frac{1}{s}\Big]=1$$

$${\mathcal L}^{-1}\Big[\frac{1}{s-\gamma_k}\Big]=e^{\gamma_kt}$$

$${\mathcal L}^{-1}\Big[\frac{s-\alpha_l}{(s-\alpha_l)^2+\beta_l^2}\Big]=e^{\alpha_lt}\cos{\beta_lt}$$

$${\mathcal L}^{-1}\Big[\frac{\beta_l}{(s-\alpha_l)^2+\beta_l^2}\Big]=e^{\alpha_lt}\sin{\beta_lt}$$