半導体とは、電気を通す導体と電気を通さない絶縁体の中間の抵抗値をもつ物質です。
電子とホール
結晶内の電子は、固有エネルギーが許されるエネルギーバンドと許されない禁止帯で構成されます。
完全に電子が詰まっているエネルギーバンド(充満帯)では、電場をかけても電子の分布は変わらないため電流は生じません。一方、一部だけ電子が詰まっているエネルギーバンド(伝導帯)では、電場をかけると電子の分布が変わるため電流が生じます。
金属のような導体では、このような伝導帯が存在するため電流を流すことができます。絶縁体では、伝導帯に電子が存在しないため電流は流れません。
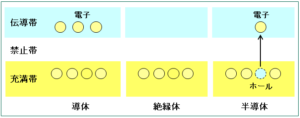
半導体では、禁止帯の幅が比較的小さいため、充満帯の電子が励起して伝導帯に移りやすく、条件により絶縁体として振舞ったり、導体として振舞ったりします。電子が励起した後の充満帯の空席をホール(正孔)と呼びます。
半導体の種類
不純物を含む半導体は真性半導体と呼ばれ、充満帯の電子が伝導帯に上がるので、伝導帯の電子の数 $n$ と充満帯(価電子帯)のホールの数 $p$ は同数 $n=p$ となります。
一方、不純物を含む半導体では電子の数とホールの数は等しくなく、電子の数がホールより多い半導体($n\gt p$)をn型半導体、ホールの数が電子より多い半導体($p\gt n$)をp型半導体と呼びます。
つまり、電流の担い手あるキャリヤが、n型半導体では主に負($\mathrm{negative}$)、p型半導体では主に正($\mathrm{positive}$)となります。
n型半導体
n型半導体の例としては、Ⅳ族の元素である Si(ケイ素)にⅤ族の元素である As(ヒ素)をごく少量の入れた場合です。
Ⅳ族の Si は4個の価電子を持ち、Ⅴ族の As は5個の価電子を持つため、各原子間で2個の電子による共有結合を行うと、As の電子が1個余ります(下図左)。
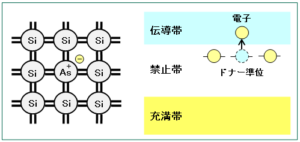
この余分な電子は、伝導帯のすぐ下の禁止帯にエネルギー準位(ドナー準位)を持つため、常温の熱エネルギーでも容易に伝導帯に励起することができます(上図右)。
As などの伝導帯に電子を与える原子はドナーと呼ばれ、ドナーを多く含む半導体では、ドナー準位から伝導帯に上がった電子が主として電流のキャリヤとなり、ホールはほとんど寄与しません。
p型半導体
p型半導体の例としては、Ⅳ族の元素である Si にⅢ族の元素である In(インジウム)をごく少量の入れた場合です。
Ⅳ族の Si は4個の価電子を持ち、Ⅲ族の In は3個の価電子を持つため、各原子間で2個の電子による共有結合を行うと、In の電子が1個不足します。この不足分は付近の電子で補われるため、In の周りにホールが作られます(下図左)。
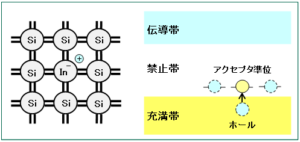
このホールは、充満帯(価電子帯)のすぐ上の禁止帯にエネルギー準位(アクセプタ準位)を持つため、充満帯(価電子帯)の電子は、常温の熱エネルギーでも容易にアクセプタ準位に励起することができます(上図右)。
In などの充満帯(価電子帯)にホールを与える原子はアクセプタと呼ばれ、アクセプタを多く含む半導体では、アクセプタ準位から価電子帯に移ったホールが主として電流のキャリヤとなり、電子はほとんど寄与しません。
電子の運動方程式
エネルギーバンド内の電子の運動方程式は以下になります。この式はニュートンの運動の第2法則に相当し、${\bf F}$ は結晶内の電子に働く外力や結晶格子からの力になります。
$$\hbar\frac{d{\bf k}}{dt}={\bf F} -①$$
①を導く
時間 $\delta t$ の間に力 $F$ によって電子になされる仕事は、
$$\delta\epsilon=Fv_g\delta t -(1)$$
ここで $v_g$ は群速度で、以下で表されます。
$$v_g=\frac{d\omega}{dk} -②$$
これらと関係式 $\epsilon=\hbar\omega$ を使うと、
$$\delta\epsilon=\frac{d\epsilon}{d\omega}\frac{d\omega}{dk}\delta k=\hbar v_g\delta k$$
これと (1) を等しいと置くと①が得られます。
$$F\delta t=\hbar\delta k$$
有効質量
有効質量とは、結晶内の電子の見かけ上の質量です。有効質量をとすると、結晶内の電子の運動方程式は以下になります。
$$m^*\frac{d{\bf v}_g}{dt}={\bf F} -③$$$$\frac{1}{m^*}\equiv\frac{1}{\hbar^2}\frac{d^2\epsilon}{dk^2}$$
③を導く
$\epsilon=\hbar\omega$ の両辺を $k$ で微分すると、
$$\hbar\frac{d\omega}{dk}=\frac{d\epsilon}{dk}$$
②を使い、両辺を時間微分すると、
$$\hbar\frac{dv_g}{dt}=\frac{d}{dk}\frac{d\epsilon}{dt}=\frac{d}{dk}\frac{dk}{dt}\frac{d\epsilon}{dk}$$
左辺に①を使うと、③が導かれることが分かります。
$$\frac{dv_g}{dt}=\frac{1}{\hbar^2}\frac{d^2\epsilon}{dk^2}F=\frac{1}{m^*}F$$




