ガウス・グリーンの定理
ガウス・グリーンの定理は、閉曲面 $S$ で囲まれた空間の領域を $V$ 、曲面の外向き法線の方向余弦を($l , m , n$)、微分可能な関数を $f$ 、$g$ 、$h$ としたときに、以下の関係が成り立つことを示します。
$$\int_V\Big(\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}+\frac{\partial h}{\partial z}\Big)dV=\int_S(fl+gm+hn)dS -①$$
ガウス・グリーンの定理を導く
各項毎に成り立てばよいので、以下の式を証明します。
$$\int_V\frac{\partial h}{\partial z}dV=\int_ShndS -(1)$$
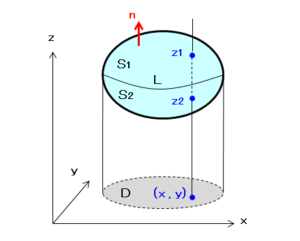
閉曲面 $S$ の $xy$-平面への投影を $D$ とし、$D$ を底とした円筒形と閉曲面 $S$ が接して作られる閉曲線を $L$ とします。$L$ で閉曲面 $S$ を上下に分けて、上側を $S_1$ 、下側を $S_2$ とし、$D$ 内の点($x,y$)からの垂線と $S_1$ 、$S_2$ との交点を $z_1$ 、$z_2$ とします。
(1)の左辺を $z$ で積分すると、
$$\int_V\frac{\partial h}{\partial z}dxdydz=\int_D\Big(h(x,y,z_1)-h(x,y,z_2)\Big)dxdy$$$$=\int_{S_1}h(x,y,z)ndS+\int_{S_2}h(x,y,z)ndS$$$$=\int_Sh(x,y,z)ndS$$
$n$ を閉曲面 $S$ の法線($dxdy=ndS$)とすると、第2項の符号が反転します。これにより、(1)が得られることが分かります。
グリーンの定理
グリーンの定理は、微分可能な関数を $\phi$ 、$\psi$ 、法線方向の微分を $\partial/\partial n$ としたときに、以下の関係が成り立つことを示します。
$$\int_V\Big(\phi\Delta\psi+\frac{\partial\phi}{\partial x}\frac{\partial\psi}{\partial x}+\frac{\partial\phi}{\partial y}\frac{\partial\psi}{\partial y}+\frac{\partial\phi}{\partial z}\frac{\partial\psi}{\partial z}\Big)dV=\int_S\phi\frac{\partial\psi}{\partial n}dS -②$$$$\int_V(\phi\Delta\psi-\psi\Delta\phi)dV=\int_S\Big(\phi\frac{\partial\psi}{\partial n}-\psi\frac{\partial\phi}{\partial n}\Big)dS -③$$
グリーンの定理を導く
以下のように置き換えることにより、
$$f\equiv\phi\frac{\partial\psi}{\partial x} , g\equiv\phi\frac{\partial\psi}{\partial y} , h\equiv\phi\frac{\partial\psi}{\partial z}$$
①の左辺は、
$$\int\left(\frac{\partial}{\partial x}\Big(\phi\frac{\partial\psi}{\partial x}\Big)+\frac{\partial}{\partial y}\Big(\phi\frac{\partial\psi}{\partial y}\Big)+\frac{\partial}{\partial z}\Big(\phi\frac{\partial\psi}{\partial z}\Big)\right)dV$$$$=\int\Big(\phi\Delta\psi+\frac{\partial\phi}{\partial x}\frac{\partial\psi}{\partial x}+\frac{\partial\phi}{\partial y}\frac{\partial\psi}{\partial y}+\frac{\partial\phi}{\partial z}\frac{\partial\psi}{\partial z}\Big)dV$$
①の右辺は、
$$\int_S(l\phi\frac{\partial\psi}{\partial x}+m\phi\frac{\partial\psi}{\partial y}+n\phi\frac{\partial\psi}{\partial z})dS=\int_S\phi\frac{\partial\psi}{\partial n}dS$$
以上より②が得られます。尚、法線方向の微分は以下で定義されます。
$$\frac{\partial}{\partial n}\equiv l\frac{\partial}{\partial x}+m\frac{\partial}{\partial y}+n\frac{\partial}{\partial z}$$
一方、③については、②で $\phi$ と $\psi$ を入れ替え、
$$\int_V\Big(\psi\Delta\phi+\frac{\partial\psi}{\partial x}\frac{\partial\phi}{\partial x}+\frac{\partial\psi}{\partial y}\frac{\partial\phi}{\partial y}+\frac{\partial\psi}{\partial z}\frac{\partial\phi}{\partial z}\Big)dV=\int_S\psi\frac{\partial\phi}{\partial n}dS$$
②との差分を取ることで得られます。
ガウスの定理
ガウスの定理は以下で表されますが、
$$\int\nabla\cdot{\bf A}dV=\int A_ndS -④$$
①において、
$$f\equiv A_x , g\equiv A_y , h\equiv A_n$$
と置き換え、
$$\int_V\Big(\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}\Big)dV=\int_S(A_xl+A_ym+A_zn)dS$$
${\bf A}$の法線方向の成分 $A_n$ を以下で定義すると④が得られます。
$$A_xl+A_ym+A_zn={\bf A}\cdot{\bf n}\equiv A_n$$




