ダイオード
ダイオードとは、電子回路において整流作用をもつ電子部品です。最初のダイオードは2極真空管ですが、本記事では半導体ダイオード(以下、ダイオード)を扱います。
ダイオードには2つの端子があり、アノード(Anode)とカソード(Cathode)と呼ばれます。アノードからカソードへは電流は流れますが、逆方向へはほとんど流れません。
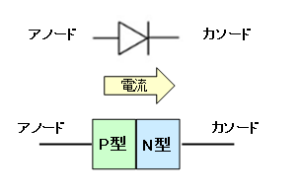
ダイオードは、P型半導体とN型半導体を組合せることで作ることができます。
PN接合
P型半導体とN型半導体のエネルギー準位を以下に示します。P型半導体のアクセプタ準位(P型半導体のフェルミ準位の近傍)は価電子帯の近くにあり、N型半導体のドナー準位(N型半導体のフェルミ準位の近傍)は伝導帯の近くあります。
ホール(プラスの電荷)のポテンシャルエネルギーは、外部の真空を基準として、上に行くほど低く、下に行くほど高くなります。これに対し、電子(マイナスの電荷)のポテンシャルエネルギーは、上に行くほど高く、下に行くほど低くなります。
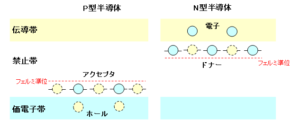
P型半導体とN型半導体を接合すると、接合面に近いP型半導体のホールは拡散してN型半導体に移り、アクセプタは電子を取り込んでマイナスイオンになります。一方、接合面に近いN型半導体の電子は拡散してP型半導体に移り、ドナーは電子を放出してプラスイオンになります。
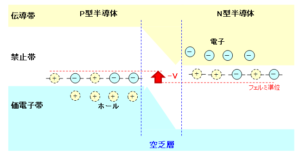
このため、P型半導体はマイナス化し、N型半導体はプラス化するため、P型半導体の電位に比べ、N型半導体の電位は下にずれるような形になります。そして下図のように、P型半導体とN型半導体のフェルミ準位が一致するところで平衡状態となります。
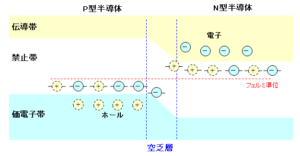
このように、P型半導体とN型半導体の接合面は一定の電位差(障壁電位差)が保たれ、伝導電子もホールも存在しない部分になります。この部分は空乏層と呼ばれます。
P型半導体側の空乏層の幅 $W_p$ とN型半導体の空乏層の幅 $W_n$ の関係は、アクセプタの密度 $N_a$ 、ドナーの密度 $N_d$ と以下の関係あります。(導出)
$$N_aW_p=N_dW_n -①$$
これより、アクセプタが少なくドナーが多いPN接合の場合($N_a\lt N_d$)、空乏層はP型半導体に片寄り($W_p\gt W_n$)、アクセプタが多くドナーが少ないPN接合の場合($N_a\gt N_d$)、その逆になる($W_p\lt W_n$)ことが分かります。
また、空乏層全体の幅は以下で表されます。$\Delta\phi$ はP型半導体とN型半導体の電位差です。(導出)
$$W=W_n+W_p=\sqrt{\frac{2\epsilon\Delta\phi(N_a+N_d)}{eN_aN_d}} -②$$
電流特性
PN接合部分を流れる電流は、N型半導体からP型半導体に移動する電子 $J_n^p$ とP型半導体からN型半導体に移動するホール $J_p^n$ の和で表されます。
$$J=J_n^p(0)+J_p^n(0) -③$$
ダイオードは、P型半導体(アノード)からN型半導体(カソード)へは電流は流れますが、逆方向へはほとんど流れません。P型半導体の電圧を $V$(プラス=順方向)とすると、ダイオードの電流特性は以下で表されます。(導出)
$$J=J_s\Big(e^{eV/kT}-1\Big) -④$$$$J_s\equiv Se\left(n_0^p\sqrt{\frac{D_n}{\tau^p}}+p_0^n\sqrt{\frac{D_p}{\tau^n}}\right)$$
ここで、$n_0^p$ はP型半導体中の電子密度、$p_0^n$ はN型半導体中のホール密度、$D_n$ と $D_p$ は電子とホールの拡散係数、$\tau^p$ はP型半導体内の電子の平均寿命、$\tau^n$ はN型半導体内のホールの平均寿命、$S$ はPN接合の面積です。
④の関係式をイメージで表すと以下になります。まず、P型半導体(アノード)に電圧 $V$(順方向)をかけると、P型半導体のフェルミ準位は下にずれる形になり、空乏層の電位差は小さく、幅は狭くなります。このため、キャリアの電子とホールは移動し易くなります。
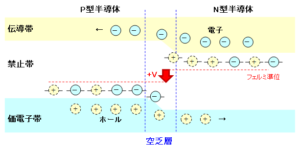
一方、N型半導体(カソード)に電圧 $V$(逆方向)をかけると、P型半導体のフェルミ準位は上にずれる形になり、空乏層の電位差は大きく、幅は広くなります。このため、キャリアの電子とホールは移動がより困難になります。
導出
①を導く
PN接合面を平面とし、PN接合面に垂直に $x$ 軸をとります。ポアソンの方程式
$$\nabla^2\phi=-\frac{\rho}{\epsilon}$$
をP型半導体側とN型半導体側で立てると、
$$\mbox{P型:} \frac{d^2\phi(x)}{dx^2}=\frac{eN_a}{\epsilon}$$$$\mbox{N型:} \frac{d^2\phi(x)}{dx^2}=-\frac{eN_d}{\epsilon}$$
これらを解くと以下になります。
$$\mbox{P型:} \phi(x)=\phi_p+\frac{eN_a}{2\epsilon}(x+W_p)^2 -(1)$$$$\mbox{N型:} \phi(x)=\phi_n-\frac{eN_d}{2\epsilon}(x-W_n)^2 -(2)$$
(1) と (2) の微分を行い、
$$\mbox{P型:} \phi'(x)=\frac{eN_a}{\epsilon}(x+W_p)$$$$\mbox{N型:} \phi'(x)=-\frac{eN_d}{2\epsilon}(x-W_n)$$
これらの $x=0$ での値、
$$\mbox{P型:} \phi'(0)=\frac{eN_a}{\epsilon}W_p$$$$\mbox{N型:} \phi'(0)=\frac{eN_d}{2\epsilon}W_n$$
は等しくなるため、①が得られます。
$$N_aW_p=N_dW_n$$
②を導く
(1) と (2) で $x=0$ とすると、
$$\mbox{P型:} \phi(0)=\phi_p+\frac{eN_a}{2\epsilon}W_p^2$$$$\mbox{N型:} \phi(0)=\phi_n-\frac{eN_d}{2\epsilon}W_n^2$$
ここで、P型半導体での電位差 $\Delta\phi_p$ とN型半導体での電位差 $\Delta\phi_n$ を以下で定義すると、
$$\Delta\phi=\Delta\phi_p+\Delta\phi_n -(3)$$$$\Delta\phi_p\equiv\phi(0)-\phi_p=\frac{eN_a}{2\epsilon}W_p^2 -(4)$$$$\Delta\phi_n\equiv\phi_n-\phi(0)=\frac{eN_d}{2\epsilon}W_n^2 -(5)$$
(4) に ①と (5)を代入して $W_p$ と $W_n$ を消去すると、
$$N_a\Delta\phi_p=N_d\Delta\phi_n$$
これより、P型半導体の電位差とN型半導体の電位差はアクセプタとドナーの密度に依るため、(3) を考慮して、
$$\Delta\phi_p=\frac{N_d}{N_a+N_d}\Delta\phi -(6)$$$$\Delta\phi_n=\frac{N_a}{N_a+N_d}\Delta\phi -(7)$$
空乏層の幅を計算すると、(4)と(5)より、
$$W=W_p+W_n=\sqrt{\frac{2\epsilon}{eN_a}\Delta\phi_p}+\sqrt{\frac{2\epsilon}{eN_d}\Delta\phi_n}$$
(6)と(7)を代入すると、②が得られます。
$$W=\sqrt{\frac{2\epsilon}{eN_a}\frac{N_d}{N_a+N_d}\Delta\phi}+\sqrt{\frac{2\epsilon}{eN_d}\frac{N_a}{N_a+N_d}\Delta\phi}$$$$=\sqrt{\frac{2\epsilon\Delta\phi}{e(N_a+N_d)}}\Big(\sqrt{\frac{N_d}{N_a}}+\sqrt{\frac{N_a}{N_d}}\Big)$$$$=\sqrt{\frac{2\epsilon\Delta\phi(N_a+N_d)}{eN_aN_d}}$$
③を導く
電子とホールの密度の変化は拡散方程式で表されます。P型半導体内の電子 $n^p$ とN型半導体内のホール $p^n$ の拡散方程式はそれぞれ以下になります。
$$D_n\frac{\partial^2n^p(x)}{\partial x^2}=\frac{n^p(x)-n_0^p}{\tau^p} -(8)$$$$D_p\frac{\partial^2p^n(x)}{\partial x^2}=\frac{p^n(x)-p_0^n}{\tau^n} -(9)$$
(8) について、$x=0$ で $n^p(0)$ 、$x=-\infty$ で $n^p_0$ となる条件で解くと、
$$n^p(x)=n^p_0+\Big(n^p(0)-n^p_0\Big)e^{x/\sqrt{D_n\tau^p}} -(10)$$
(9) について、$x=0$ で $p^n(0)$ 、$x=\infty$ で $p^n_0$ となる条件で解くと、
$$p^n(x)=p^n_0+\Big(p^n(0)-p^n_0\Big)e^{-x/\sqrt{D_p\tau^n}} -(11)$$
電流はキャリアの勾配で表されるため、P型半導体内の電子による電流 $J_n^p$ とN型半導体内のホールによる電流 $J_p^n$ はそれぞれ以下になります。
$$J_n^p(x)=SeD_n\frac{dn^p}{dx} -(12)$$$$J_p^n(x)=SeD_p\frac{dp^n}{dx} -(13)$$
(10) を (12) に代入し、(11) を (13) に代入すると、
$$J_n^p(x)=Se\Big(n^p(0)-n^p_0\Big)\sqrt{\frac{D_n}{\tau^p}}e^{x/\sqrt{D_n\tau^p}} -(14)$$$$J_p^n(x)=Se\Big(p^n(0)-p^n_0\Big)\sqrt{\frac{D_p}{\tau^n}}e^{-x/\sqrt{D_p\tau^n}} -(15)$$
電圧0の場合、P型半導体内の電子密度 $n^p_0$ とN型半導体内の電子密度 $n^n_0$ はボルツマン分布に従います。
$$\frac{n^p_0}{n^n_0}=e^{-e\Delta\phi/kT} -(16)$$
同様に、N型半導体内のホール密度 $p^n_0$ とP型半導体内のホール密度 $p^p_0$ もボルツマン分布に従います。
$$\frac{p^n_0}{p^p_0}=e^{-e\Delta\phi/kT} -(17)$$
ダイオードの順方向に電圧 $V$ をかけると、電位差は $\Delta\phi-V$ になります。このとき、P型半導体内に移動してくる電子密度を $n^p(0)$ 、N型半導体内に移動してくるホール密度を $p^n(0)$ とすると、これらもボルツマン分布に従うと考えられます。
$$n^p(0)=n^n_0e^{-e(\Delta\phi-V)/kT} -(18)$$$$p^n(0)=p^p_0e^{-e(\Delta\phi-V)/kT} -(19)$$
(16) を (18) に代入し、(17) を (19) に代入すると、
$$n^p(0)=n^p_0e^{eV/kT} -(20)$$$$p^n(0)=p^n_0e^{eV/kT} -(21)$$
(20) を (14) に代入し、(21) を (15) に代入すると、
$$J_n^p(0)=Sen^p_0\sqrt{\frac{D_n}{\tau^p}}\Big(e^{eV/kT}-1\Big) -(22)$$$$J_p^n(0)=Sep^n_0\sqrt{\frac{D_p}{\tau^n}}\Big(e^{eV/kT}-1\Big) -(23)$$
これらを③を代入すると、
$$J=Se\left(n_0^p\sqrt{\frac{D_n}{\tau^p}}+p_0^n\sqrt{\frac{D_p}{\tau^n}}\right)\Big(e^{eV/kT}-1\Big)$$
これより⓸が得られることが分かります。




