リトルの公式とは
リトルの公式とは、定常的な待ち行列システムにおいて、系内(店内)の平均客数と平均滞在時間、あるいは、平均待ち行列長と平均待ち時間の関係を表したものです。
待ち行列で用いられる変数を以下にまとめます。
- $L(t)$:系内客数
- $W(t)$:滞在時間
- $L_q(t)$:待ち行列長
- $W_q(t)$:待ち時間
- $S(t)$:窓口客数($=L-L_q$)
- $\sigma$:サービス時間($=W-W_q$)
- $\lambda$:到着率(単位時間当たりの平均到着客数)
- $\mu$:処理能力($=1/\sigma$)
- $a$:呼量、アーラン($=\lambda\sigma$)
- $c$:窓口数
- $\rho$:使用率($=a/c$)
平均客数と滞在時間の関係
系内の平均客数 $\bar{L}$ は、平均滞在時間 $\bar{W}$ と到着率 $\lambda$ の積に等しくなります(導出)。
$$\bar{L}=\lambda\bar{W} -①$$
ここで、$\bar{L}$ と $\bar{W}$ は以下で定義されます。
$$\bar{L}\equiv\lim_{t\to\infty}\int_0^tL(\tau)d\tau$$$$\bar{W}\equiv\lim_{t\to\infty}\int_0^tW(\tau)d\tau$$
待ち行列長と待ち時間の関係
平均待ち行列長 $\bar{L}_q$ は、平均待ち時間 $\bar{W}_q$ と到着率 $\lambda$ の積に等しくなります。
$$\bar{L}_q=\lambda\bar{W}_q -②$$
ここで、$\bar{L}_q$ と $\bar{W}_q$ は以下で定義されます。
$$\bar{L}_q\equiv\lim_{t\to\infty}\int_0^tL_q(\tau)d\tau$$$$\bar{W}_q\equiv\lim_{t\to\infty}\int_0^tW_q(\tau)d\tau$$
窓口客数とサービス時間
窓口客数 $\bar{S}$ とサービス時間 $\bar{\sigma}$ の定義と①②より以下の関係が得られます。
$$\bar{S}=\lambda\bar{\sigma}$$
尚、右辺の $\lambda\bar{\sigma}$ は呼量と呼ばれており、これを窓口数 $c$ で割った量は使用率 $\rho$ と呼ばれています。
$$\rho\equiv\frac{\lambda\bar{\sigma}}{c}=\frac{\lambda}{c\mu}$$
リトルの公式を導く
以下、窓口が1つ($c=1$)の場合でリトルの公式を求めます。この場合、$\rho=\lambda/\mu$ となります。
①を導く
系内に客数を $n$ 、その確率を $P_n$ とすると、系が定常状態の場合は、ある時刻 $t$ での $P_n$ と時刻 $t+\Delta t$ での $P_n$ が等しくなるため、
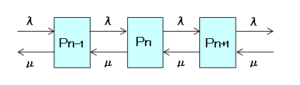
$$\frac{dP_n}{dt}=\lambda P_{n-1}-\mu P_n-\lambda P_n+\mu P_{n+1}=0 -(1)$$
尚、$n=0$ の場合は以下で定義します。
$$\frac{dP_0}{dt}=-\lambda P_0+\mu P_1=0 -(2)$$
(1)と(2)より順番に求めると、
$$P_1=\rho P_0$$$$P_2=(1+\rho)P_1-\rho P_0=\rho^2P_0$$$$\cdots$$$$P_n=\rho^nP_0 -(3)$$
$P_n$ の全ての和は1であるため、
$$\sum_{n=0}^\infty P_n=P_0+\rho P_0+\rho^2P_0+\cdots=\frac{P_0}{1-\rho}=1$$
これを(3)に代入すると、
$$P_n=\rho^n(1-\rho)$$
系内の客数 $L$ を計算すると、
$$L=\sum_{n=0}^\infty nP_n=\sum_{n=0}^\infty n\rho^n(1-\rho)$$$$=(1-\rho)(\rho+2\rho^2+3\rho^3+\cdots)$$
ここで、
$$A\equiv\rho+2\rho^2+3\rho^3+4\rho^4+\cdots$$
と置き、$\rho$ 倍すると、
$$\rho A=\rho^2+2\rho^3+3\rho^4+4\rho^5+\cdots$$
これらの差を取ると、
$$(1-\rho)A=\rho+\rho^2+\rho^3+\rho^4+\cdots=\frac{\rho}{1-\rho}$$
従って、
$$L=\frac{\rho}{1-\rho} -(4)$$
一方、系内の客数が $n$ の場合、次に入ってきた客の待ち時間は $(n+1)/\mu$ であるため、系の滞在時間 $W$ を計算すると、
$$W=\sum_{n=1}^\infty\frac{n+1}{\mu}P_n=\sum_{n=1}^\infty\frac{n+1}{\mu}\rho^n(1-\rho)$$$$=\frac{1-\rho}{\mu}(\rho+2\rho^2+3\rho^3+\cdots)+\frac{1}{\mu}$$$$=\frac{\rho}{\mu(1-\rho)}+\frac{1}{\mu}=\frac{1}{\mu(1-\rho)} -(5)$$
(4)と(5)より①が導かれます。
$$L=\lambda W$$




