量子エラー訂正
量子エラー訂正とは、量子コンピュータの計算の過程で発生してしまうエラーを訂正する技術です。量子エラーとは、以下のように量子ビットが変化してしまうことを指します。
$$c_1\ket{0}+c_2\ket{1} \to c_1’\ket{0}+c_2’\ket{1}$$
このような量子エラーは、$(c_1,c_2)$ から $(c_1^{‘},c_2^{‘})$ への変換として2×2の行列で表すことができます。
$$\left(\begin{array}{ccc} c_1^{‘} \\ c_2^{‘} \end{array}\right)=
\left(\begin{array}{ccc} a & b \\ c & d \end{array}\right)
\left(\begin{array}{ccc} c_1 \\ c_2 \end{array}\right)$$
任意の2×2行列は、以下の4つの行列の線形結合で書くことができます。ここで $X$ と $Z$ はパウリ行列(パウリゲート)です。
$$\left(\begin{array}{ccc} a & b \\ c & d \end{array}\right)=\alpha I+\beta X+\gamma Z+\delta XZ$$$$I=\left(\begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array}\right)$$$$X=\left(\begin{array}{ccc} 0 & 1 \\ 1 & 0 \end{array}\right)$$$$Z=\left(\begin{array}{ccc} 1 & 0 \\ 0 & -1 \end{array}\right)$$$$XZ=\left(\begin{array}{ccc} 0 & -1 \\ 1 & 0 \end{array}\right)$$
従って、任意の量子エラーは以下の4つの場合の重ね合わせと考えることができます。
- $I$:量子エラー無し
- $X$:ビット反転エラー
- $Z$:位相反転エラー
- $XZ$:ビット+位相反転エラー
以下は、ビット反転エラーと位相反転エラーについて説明します。
ビット反転エラー
ビット反転エラーとは、パウリゲート $X$ で変換されるような $\ket{0}\to\ket{1}$ 、$\ket{1}\to\ket{0}$ となってしまうエラーで、通常の電子回路で発生するエラーです。
$$c_1\ket{0}+c_2\ket{1} \to c_1\ket{1}+c_2\ket{0}$$
$$X\left(\begin{array}{ccc} 0 \\ 1 \end{array}\right)=
\left(\begin{array}{ccc} 0 & 1 \\ 1 & 0 \end{array}\right)
\left(\begin{array}{ccc} 0 \\ 1 \end{array}\right)
=\left(\begin{array}{ccc} 1 \\ 0 \end{array}\right)$$
このようなエラーを検出するために以下のような量子回路を用います。ここで、 $\oplus$ は制御NOTゲート、$[X]$ はXゲート、$[0/1]$ はビットの読み出しを表します。

受信側の制御NOTゲートでは、制御ビット $\ket{\psi}$ が0の場合は、標的ビット $\ket{0}$ は変化せず、制御ビットが1の場合は標的ビットは反転します。従って、以下のように量子もつれが起きた状態で送信されます。3つのビットの内、左端のビット(第1ビット)を $\ket{\psi}$ とします。
$$\ket{\psi}=\ket{0} \to \ket{000}$$$$\ket{\psi}=\ket{1} \to \ket{111}$$
この3ビットの中の1ビットが送信中にエラーが起こったと仮定します。しかし、量子ビットを直接確認することはできないため、受信側で制御NOTゲートを通すことで、間接的にどのビットにエラーが起きたかを確認します。
| 送信側 | 受信側 | $[0/1]$ 出力 | |
| 第2ビット | 第3ビット | ||
| $\ket{000}$ |
$\ket{100}$ | $1$ | $1$ |
| $\ket{010}$ | $1$ | $0$ | |
| $\ket{001}$ | $0$ | $1$ | |
| エラー無し | $0$ | $0$ | |
| $\ket{111}$ |
$\ket{011}$ | $1$ | $1$ |
| $\ket{101}$ | $1$ | $0$ | |
| $\ket{110}$ | $0$ | $1$ | |
| エラー無し | $0$ | $0$ | |
これより送信側のビットに関係なく、第1ビットにエラーが発生した場合は、$[0/1]$ 出力の第2ビットと第3ビットが両方 $1$ になることが分かります。$[X]$ は制御 $X$ ゲートで、制御ビット(第2ビットと第3ビット)が $11$ の場合にビット反転を行います。
$$c_1\ket{1}+c_2\ket{0} \to c_1\ket{0}+c_2\ket{1}$$
$$X\left(\begin{array}{ccc} 1 \\ 0 \end{array}\right)=
\left(\begin{array}{ccc} 0 & 1 \\ 1 & 0 \end{array}\right)
\left(\begin{array}{ccc} 1 \\ 0 \end{array}\right)
=\left(\begin{array}{ccc} 0 \\ 1 \end{array}\right)$$
以上により、エラー訂正が行えることが分かります。
位相反転エラー
位相反転エラーとは、パウリゲート $Y$ で変換されるような $\ket{0}\to\ket{0}$ 、$\ket{1}\to-\ket{1}$ となってしまうエラーで、量子回路特有のエラーです。
$$c_1\ket{0}+c_2\ket{1} \to c_1\ket{0}-c_2\ket{1}$$
$$Y\left(\begin{array}{ccc} 0 \\ 1 \end{array}\right)=
\left(\begin{array}{ccc} 1 & 0 \\ 0 & -1 \end{array}\right)
\left(\begin{array}{ccc} 0 \\ 1 \end{array}\right)
=\left(\begin{array}{ccc} 0 \\ -1 \end{array}\right)$$
このようなエラーを検出するために以下のような量子回路を用います。ここで、$[H]$ はアダマールゲートを表します。
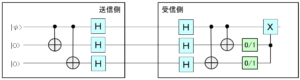
アダマールゲートは量子ビットを以下のように変換するので、
$$\ket{0} \to \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\equiv\ket{+}$$$$\ket{1} \to \frac{1}{\sqrt{2}}(\ket{0}-\ket{1})\equiv\ket{-}$$
受信側では以下のように変換されて送信されます。
$$\ket{\psi}=\ket{0} \to \ket{000} \to \ket{+++}$$$$\ket{\psi}=\ket{1} \to \ket{111} \to \ket{-\,-\,-}$$
このようにすると、位相反転エラーは、$\ket{+}\to\ket{-}$ 、$\ket{+}\to\ket{-}$ のようなビット反転エラーとして考えることができます。エラーがない場合は、受信側で制御NOTゲートを通すと、以下のように変換されます。
$$\ket{+++} \to \ket{000}$$$$\ket{-\,-\,-} \to \ket{111}$$
従って、送信中の1ビットのエラーは、ビット反転エラーの場合と同様の考え方で、$X$ ゲートで変換することによってエラー訂正を行うことができます。




