ステファン・ボルツマンの法則
ステファン・ボルツマンの法則とは、黒体放射(空洞放射)のエネルギー密度は温度の4乗に比例するという法則です。これは、星の光度と表面温度の関係に応用することができます。単位時間に単位面積に放出されるエネルギー $K$ と温度 $T$ には以下の関係があります。
$$K(T)=\sigma T^4$$
ここで $\sigma$ はステファン・ボルツマン定数と呼ばれ、以下の値を持ちます。
$$\sigma=5.67×10^{-8} Wm^{-2}K^{-4}$$
星の光度と見かけの明るさ
星の光度とは、天球全体から単位時間に放射されるエネルギーで、天体の真の明るさを示します。一方、光源から離れるほど見かけの明るさ(輻射流束)は暗くなります。天体からの距離を $r$ とすると、光度 $L$ と輻射流束 $K$ の関係は以下になります。
$$K=\frac{L}{4\pi r^2}$$
星の半径を $R$ とすると、ステファン・ボルツマンの法則より、星の光度と温度の関係は以下で表すことができます。
$$L=4\pi R^2\sigma T^4$$
式の導出
以下、ステファン・ボルツマンの法則を分子運動論的に導きます。
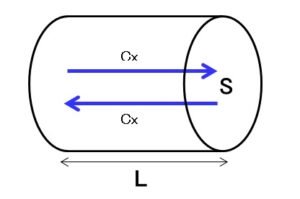
弾性衝突を仮定すると、運動量 $P_x=mc_x$ を持つ分子が壁に与える力積は $2P_x$、次の衝突までの時間は $2L/c_x$ であるので、壁の面積 $S$ 、圧力 $p$ との関係は以下になります。
$$\sum 2P_x\frac{c_x}{2L}=Sp -①$$
電磁場のエネルギー $U=c|{\bf P}|$ を成分で表すと、
$$U\frac{{\bf c}}{c}=c|{\bf P}|$$
となるため、$x$ 成分に注目すると $P_x=Uc_x/c^2$ となるため、①より以下になります。
$$p=\frac{1}{V}\sum U\frac{c_x^2}{c^2}$$
ここで体積を $V=SL$ としています。空間の等方性を仮定すると、$c^2=c_x^2+c_y^2+c_z^2$ で $\sum c_x^2=\sum c_y^2=\sum c_z^2$ であるため以下が導かれます。
$$p=\frac{U}{3V}=\frac{1}{3}u(T) -②$$
$u$ は単位体積当たりの電磁場のエネルギーで、この式は電磁波が物体に及ぼす圧力を示します。この式を、熱力学の関係式、
$$dU=TdS-pdV$$$$\Big(\frac{\partial U}{\partial V}\Big)_T=T\Big(\frac{\partial S}{\partial V}\Big)_T-p$$
これにマクスウェルの関係式を使うと、
$$\left(\frac{\partial U}{\partial V}\right)_T=T\left(\frac{\partial p}{\partial T}\right)_V-p$$
これに②を代入すると以下の微分方程式が得られます。
$$\frac{du}{u}=4\frac{dT}{T}$$
$$u(T)\sim T^4$$
光速度を $c$ とすると、単位時間、単位面積当たりのエネルギーは $K\sim cu$ となるため、以下が求められます。
$$K(T)=\sigma T^4$$




