コーシーの積分定理
コーシーの積分定理とは、正則関数の単純閉曲線上の積分が0になることを示す定理です。単連結領域 $D$ での正則関数を $f(z)$ とすると、単純閉曲線 $C$ での積分について以下の関係が成り立ちます(①の導出)。
$$\int_Cf(z)dz=0 -①$$
コーシーの積分定理を導く
①の左辺に以下の定義を代入します。
$$f(z)=u(x,y)+iv(x,y)$$$$dz=dx+idy$$
従って、
$$\int_Cf(z)dz=\int(u+iv)(dx+idy)$$$$=\int(udx-vdy)+i\int(vdx+udy)$$
$$=-\int\int\Big(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\Big)dxdy+i\int\int\big(-\frac{\partial v}{\partial y}+\frac{\partial u}{\partial x}\Big) -(1)$$
最後は次のグリーンの定理を使っています。
$$\int(Pdx+Qdy)=\int\int\Big(-\frac{\partial P}{\partial y}+\frac{\partial Q}{\partial x}\Big)dxdy$$
さらに (1) は、次のコーシー・リーマンの関係式を使うと0になることが分かります。
$$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} , \frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$$
コーシーの積分表示
コーシーの積分表示とは、不連続点の周囲の単純閉曲線上の積分が一定の値を持つことを示す定理です。単連結領域 $D$ での正則関数を $f(z)$ とすると、以下の関係が成り立ちます(②の導出)。
$$\int_C\frac{f(z)}{z-z_0}dz=2\pi if(z_0) -②$$
尚、左辺は不連続点($z=z_0$)を左回り(反時計回り)する周回積分になります。右回り(時計回り)の場合は符号が逆になります。
また、コーシーの積分表示と同じ条件のもとで、$f(z)$ は限りなく微分可能であるため、任意の点 $a$ について以下で表されます(③の導出)。
$$f^{(n)}(a)=\frac{n!}{2\pi i}\int_C\frac{f(z)}{(z-a)^{n+1}}dz -③$$
コーシーの積分表示を導く
②の左辺の被積分関数は $z=z_0$ で不連続であるため、下図のような積分経路を考えます。コーシーの積分定理より、経路を一周する積分は0になります。
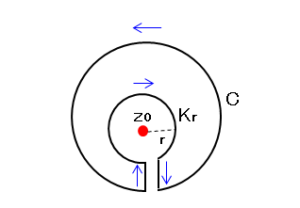
2つの周回路 $C$ 、$K_r$ を結ぶ経路は互いに相殺されるため、コーシーの積分定理は以下で表されます。
$$0=\int_C\frac{f(z)}{z-z_0}dz+\int_{K_r^{-1}}\frac{f(z)}{z-z_0}dz$$$$=\int_C\frac{f(z)}{z-z_0}dz-\int_{K_r}\frac{f(z)}{z-z_0}dz$$
尚、内側の周回路 $K_r$ は左回り、$K_r^{-1}$ は右回りを表し、積分の符号は反転します。ここで $z=z_0+re^{i\theta}$ と置くと、$dz=ire^{i\theta}d\theta$ となるため、第2項に代入すると、
$$\int_C\frac{f(z)}{z-z_0}dz=\int_0^{2\pi}f(z_0+re^{i\theta})id\theta$$
右辺の積分は半径 $r$ に依存しないため、$r\to0$ とすると、
$$\int_C\frac{f(z)}{z-z_0}dz=\lim_{r\to0}\int_0^{2\pi}f(z_0+re^{i\theta})id\theta$$
$$=f(z_0)\int_0^{2\pi}id\theta=2\pi if(z_0)$$
これより②が得られます。
③を導く
②について、$|z_0-a|\lt|z-a|$ とすると、
$$\frac{1}{z-z_0}=\frac{1}{z-a}\cdot\frac{1}{1-\frac{z_0-a}{z-a}}=\frac{1}{z-a}\sum_{n=0}^\infty\Big(\frac{z_0-a}{z-a}\Big)^n$$
これを②に代入すると、
$$f(z_0)=\frac{1}{2\pi i}\int_Cf(z)\sum_{n=0}^\infty\frac{(z_0-a)^n}{(z-a)^{n+1}}dz$$$$=\frac{1}{2\pi i}\sum_{n=0}^\infty\int_Cf(z)\frac{(z_0-a)^n}{(z-a)^{n+1}}dz$$
ここで、テイラー展開の公式
$$f(z_0)=\sum_{n=0}^\infty\frac{f^{(n)}}{n!}(z_0-a)^n$$
と比較すると、③が導かれます。
$$f^{(n)}(a)=\frac{n!}{2\pi i}\int_C\frac{f(z)}{(z-a)^{n+1}}dz$$