量子ビットとは - 理数の散策路

量子ビット、量子コンピュータの回路（量子回路）を構成する素子です。量子コンピュータは、重ね合わせや量子もつれなどの量子力学的な現象を用いて、従来のコンピュータに比べ、特定の問題に対し高速な演算を実現することができます。

量子ビットの表現

量子ビットの場合は、３次元の球面上の１点として表されます。従来のビット（以下、古典ビット）は「０」か「１」の２値ですが、それに対応する量子ビットは以下のように表されます。

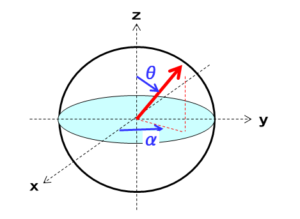
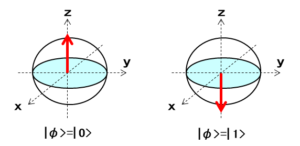
量子ビットの「０」はｚ軸のプラス向き、「１」はｚ軸のマイナス向きとして表され、ブラケット記号を用いてそれぞれ $| 0 ⟩$ と $| 1 ⟩$ と書きます。

量子ビットの特徴は、「０」と「１」の２つの状態の他に、その間の「重ね合わせ」の状態を取ることです。球面上の位置を表す変数である「 $θ$ 」と「 $α$ 」はそれぞれ、重ね合わせと位相に対応します。数式で表すと以下になります。

$| ϕ ⟩ = \cos (\frac{θ}{2}) | 0 ⟩ + e^{i α} \sin (\frac{θ}{2}) | 1 ⟩ - ①$

任意の量子ビットは「０」と「１」の重ね合わせの状態を持ちます。

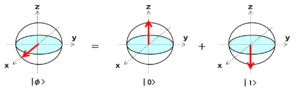
例えば、左辺の量子ビットはｘ軸のプラス方向 $(θ, α) = (π / 2, 0)$ に位置するため、以下で表されます。

$| ϕ ⟩ = \frac{1}{\sqrt{2}} | 0 ⟩ + \frac{1}{\sqrt{2}} | 1 ⟩$

赤道面上の量子ビットは「０」と「１」が同じ割合で重なり合った状態で、この量子ビットを観測すると、50％の確率で「０」と「１」が現れます。

量子ビットの位相は $α$ で表されます。

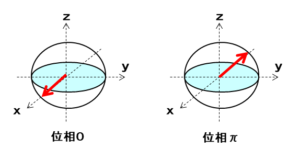
ｘ軸のプラスを向いた量子ビットの位相は０、ｘ軸のマイナスを向いた量子ビットの位相は $π$ になります。後者の量子ビット $(θ, α) = (π / 2, π)$ は以下で表されます。

$| ϕ ⟩ = \frac{1}{\sqrt{2}} | 0 ⟩ - \frac{1}{\sqrt{2}} | 1 ⟩$

各量子ビットが①のように表される任意の量子ビット $| ϕ ⟩$ であるとした場合、一般に複素数 $α, β$ によって、

$| ϕ ⟩ \equiv α | 0 ⟩ + β | 1 ⟩$

規格化条件は以下になります。

$| α |^{2} + | β |^{2} = 1$

２つの量子ビットを以下で表すと、

$| ϕ_{1} ⟩ \equiv α_{1} | 0 ⟩ + β_{1} | 1 ⟩$ $| ϕ_{2} ⟩ \equiv α_{2} | 0 ⟩ + β_{2} | 1 ⟩$

このとき、

$⟨ 0 | 0 ⟩ = ⟨ 1 | 1 ⟩ = 1$ $⟨ 0 | 1 ⟩ = ⟨ 1 | 0 ⟩ = 0$

より、量子ビットの内積は以下になります。

$⟨ ϕ_{1} | ϕ_{2} ⟩ = α_{1}^{*} α_{2} + β_{1}^{*} β_{2}$

２量子ビットの場合（例えば、 $| 01 ⟩$ ）は、それぞれの量子ビットが独立に $| 0 ⟩$ または $| 1 ⟩$ の状態を持つため、数学的には直積で表します。

$| 01 ⟩ = | 0 ⟩ \otimes | 1 ⟩$

３量子ビット以上についても同様の考え方になります。

任意の量子ビットの直積は、

$| ϕ ⟩ \otimes | ϕ ⟩ = (α | 0 ⟩ + β | 1 ⟩) \otimes (α | 0 ⟩ + β | 1 ⟩)$

この場合、以下のような４つの状態の重ね合わせとして表すことができます。

$| ϕ ϕ ⟩ = α^{2} | 00 ⟩ + α β | 01 ⟩ + β α | 10 ⟩ + β^{2} | 11 ⟩$

同様に考えると、３量子ビットは８つの状態、 $n$ 量子ビットは $2^{n}$ の状態の重ね合わせを表現できます。この原理により、量子コンピュータでは高速な並列計算を行うことが可能になります。