ドイチュ・ジョサのアルゴリズムとは

概要
量子回路
アルゴリズムの説明
ビット判定の仕組み
ステップ数の比較

概要

ドイチュとジョサは、量子コンピュータを用いることで、従来のコンピュータより圧倒的に速く計算が行える問題を最初に発見しました。この問題を解く手順（アルゴリズム）は、ドイチュ-ジョサのアルゴリズムと呼ばれています。

ドイチュ-ジョサの問題とは、あるビット配列 $X$ のパターンが以下のどちらであるかを判定する問題です。

パターンⅠ：全て「０」または全て「１」
パターンⅡ：「０」と「１」の数が同数

上記以外のパターンは考えないとする前提ですので、この問題の実用性については不明ですが、量子コンピュータの高速性が最初に証明された問題です。

量子回路

量子コンピュータで行う演算は大きく３つの段階があります。

量子の重ね合わせの状態を作る
重ね合わせの状態で並列処理を行う
結果を取り出す

この２つ目の並列処理が、量子コンピュータが圧倒的に高速である秘密です。この処理を実現する量子回路は以下になります。ここでは４ビットの配列 $X$ のパターンを検索する回路を例にとります。

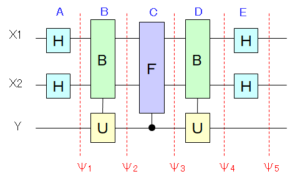
この図の、入力側の $x_1,x_2$ はアドレスビットで、$y$ は１ビットのレジスタです。４ビットの配列 $X$ は［Ｂ］に格納されており、アドレスビットにより配列 $X$ の所定のビットを指定することができます。

［Ｈ］はアダマールゲート、［Ｕ］は制御ユニタリゲート、［Ｆ］は制御位相シフトを表します。操作 $B$ と操作 $D$ は、配列 $X$ の所定のビットが制御ビット、レジスタが標的ビットです。操作 $C$ は、レジスタビットによりアドレスビットの位相が操作されます。

５つの操作の内、操作Ａで量子ビットの重ね合わせの状態を作り、操作Ｂでビット読み出しの並列処理を行い、操作Ｃ～操作Ｅで一意的な結果を取り出します。具体的な動作は後で説明します。尚、各量子ビットの入力（初期状態）は、全て０であると仮定します。

$$\Psi_0=\ket{x_1x_2,y}=\ket{00,0}$$

そして、操作Ａ～Ｄを行い、最後の $\Psi_5$ で $\ket{00}$ 以外の項が残るかどうかで、パターンⅠかパターンⅡかの判断を行います。

パターンⅠ：全て「０」または全て「１」
⇒ $\Psi_5$ に $\ket{00}$ の項のみ残る
パターンⅡ：「０」と「１」の数が同数
⇒ $\Psi_5$ に $\ket{00}$ の項以外も残る

アルゴリズムの説明

操作Ａ：重ね合わせの状態を作る

操作Ａのアダマールゲートは、量子ビットに対し以下の操作を行います。

$$H\ket{0}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})$$$$H\ket{1}=\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})$$

そのため、

$$H\ket{00,0}=\frac{1}{2}(\ket{0}+\ket{1})\otimes(\ket{0}+\ket{1}) \otimes\ket{0}$$

これを計算すると以下のように、４ビットに相当するアドレスビットのパターンが生成されます。

$$\Psi_1=\frac{1}{2}(\ket{00,0}+\ket{01,0}+\ket{10,0}+\ket{11,0})$$

操作Ｂ：配列Ｘを読み出す

操作Ｂでは、各アドレスに相当するビットをレジスタビットで読み出します。例えばビット列が［1111］（パターンⅠ）と［0110］（パターンⅡ）の場合では $\Psi_2$ は以下になります。

パターンⅠ：$X=[1111]$

$$\Psi_2=\frac{1}{2}(\ket{00,1}+\ket{01,1}+\ket{10,1}+\ket{11,1})$$

パターンⅡ：$X=[0110]$

$$\Psi_2=\frac{1}{2}(\ket{00,0}+\ket{01,1}+\ket{10,1}+\ket{11,0})$$

操作Ｂは制御ユニタリゲートで、アドレスビットで指定された配列 $X$ のビットが「１」の場合はレジスタビットが反転（$y=1$）し、「０」の場合は保持（$y=0$）されます。結果として、４ビットの配列 $X$ のレジスタへの読み出しが１回で（並列で）行われています。

操作Ｃ：結果を取り出す（１）

操作Ｃは制御位相シフトゲートで、レジスタビットが「１」の場合に、位相を反転（符号を反転）させます。２つのビットパターンで具体的に書くと以下になります。

パターンⅠ：$X=[1111]$

$$\Psi_3=\frac{1}{2}(-\ket{00,1}-\ket{01,1}-\ket{10,1}-\ket{11,1})$$

パターンⅡ：$X=[0110]$

$$\Psi_3=\frac{1}{2}(\ket{00,0}-\ket{01,1}-\ket{10,1}+\ket{11,0})$$

操作Ｄ：結果を取り出す（２）

操作Ｂと同様に、アドレスビットで指定された配列 $X$ のビットが「１」の場合はレジスタビットが反転し、「０」の場合は保持されます。結果として、レジスタビットは初期状態（０）に戻ります。

パターンⅠ：$X=[1111]$

$$\Psi_4=\frac{1}{2}(-\ket{00,0}-\ket{01,0}-\ket{10,0}-\ket{11,0})$$

パターンⅡ：$X=[0110]$

$$\Psi_4=\frac{1}{2}(\ket{00,0}-\ket{01,0}-\ket{10,0}+\ket{11,0})$$

操作Ｅ：結果を取り出す（３）

次の操作Ｄでは、再度アダマールゲートを通します。アダマールゲートは各アドレスに対して以下のような変換を行います。

$$H\ket{00}=\frac{1}{2}(\ket{0}+\ket{1})\otimes(\ket{0}+\ket{1})=\frac{1}{2}(\ket{00}+\ket{01}+\ket{10}+\ket{11})$$$$H\ket{01}=\frac{1}{2}(\ket{0}+\ket{1})\otimes(\ket{0}-\ket{1})=\frac{1}{2}(\ket{00}-\ket{01}+\ket{10}-\ket{11})$$$$H\ket{10}=\frac{1}{2}(\ket{0}-\ket{1})\otimes(\ket{0}+\ket{1})=\frac{1}{2}(\ket{00}+\ket{01}-\ket{10}-\ket{11})$$$$H\ket{11}=\frac{1}{2}(\ket{0}-\ket{1})\otimes(\ket{0}-\ket{1})=\frac{1}{2}(\ket{00}-\ket{01}-\ket{10}+\ket{11})$$

これを $\Psi_3$ の式に代入して計算します。

パターンⅠ：$X=[1111]$
この場合は、$\ket{00}$ の項のみ残ります。

$$\Psi_5=\frac{1}{4}\Big(-(\ket{00}+\ket{01}+\ket{10}+\ket{11})\otimes\ket{0}$$$$-(\ket{00}-\ket{01}+\ket{10}-\ket{11})\otimes\ket{0}$$$$-(\ket{00}+\ket{01}-\ket{10}-\ket{11})\otimes\ket{0}$$$$-(\ket{00}-\ket{01}-\ket{10}+\ket{11})\otimes\ket{0}\Big)$$$$=-\ket{00}\otimes\ket{0}　　-①$$

パターンⅡ：$X=[0110]$
この場合は、$\ket{00}$ 以外の項が残ります。

$$\Psi_5=\frac{1}{4}\Big((\ket{00}+\ket{01}+\ket{10}+\ket{11})\otimes\ket{0}$$$$-(\ket{00}-\ket{01}+\ket{10}-\ket{11})\otimes\ket{0}$$$$-(\ket{00}+\ket{01}-\ket{10}-\ket{11})\otimes\ket{0}$$$$+(\ket{00}-\ket{01}-\ket{10}+\ket{11})\otimes\ket{0}\Big)$$$$=\ket{11}\otimes\ket{0}　　-②$$

ビット判定の仕組み

①と②についてアドレスビットの項を書き出すと以下になります。

$+/-$	$+\ket{00}$	$+\ket{01}$	$+\ket{10}$	$+\ket{11}$
$+/-$	$+\ket{00}$	$-\ket{01}$	$+\ket{10}$	$-\ket{11}$
$+/-$	$+\ket{00}$	$+\ket{01}$	$-\ket{10}$	$-\ket{11}$
$+/-$	$+\ket{00}$	$-\ket{01}$	$-\ket{10}$	$+\ket{11}$

パターンⅠの場合は、［0000］か［1111］のどちらかですが、その場合は１列目が全てプラスか全てマイナスになりますので、２列目の $\ket{00}$ の項が残り、３～５列目は消去されることが分かります。

パターンⅡの場合は、「０」と「１」が混在し、１列目はプラスとマイナスが混在するため、どのような組み合わせであっても $\ket{00}$ 以外の項（３～５列目）が必ず残ることになります。

ステップ数の比較

ドイチュ-ジョサの問題を従来のコンピュータで解く場合、ビット配列を端から１つづつ確認する必要があります。例えば、４ビット（＝$2^2$ ビット）の場合、２ビットを確認して全て「０」でも、たまたまである可能性もあるので、まだパターンⅠがパターンⅡかの判断はできません。

そのため、必ずビット数の半分より１つ多い回数（２＋１回）確認する必要があります。一般に、$2^N$ ビットの配列の場合は、$2^{N-1}+1$ 回のステップが必要になります。

一方、量子回路のステップ数を数えると、操作Ａでは２つのアダマールゲートがあるので２ステップ、操作Ｂ～Ｄは３ステップ、操作Ｅは操作Ａと同様２ステップで、合計７ステップとなります。

これはビット配列の数は４ビット（$=2^2$）の場合ですが、ビット配列が増えても、操作Ａと操作Ｅのステップ数は増えるのみで、操作Ｂ～Ｄのステップ数は変わりません。一般に $2^N$ ビット配列の場合は、ステップ数は $2N+3$ 程度になります。

従来のコンピュータと量子コンピュータのステップ数を、ビット数ごとに比べると以下になります。

ビット数	ステップ数	$2^2(4)$	$2^5(32)$	$2^{10}(1024)$	$2^{20}$
従来コンピュータ	～$2^{N-1}+1$	3	17	513	523,288
量子コンピュータ	～$2N+3$	7	13	23	43