メネラウスの定理
メネラウスの定理とは、ある直線が三角形 $ABC$ の3辺 $BC,CA,AB$ またはその延長とそれぞれ点 $P,Q,R$ で交わるときに成り立つ以下の関係式です(①の導出)。
$$\frac{BP}{PC}\cdot\frac{CQ}{QA}\cdot\frac{AR}{RB}=1 -①$$
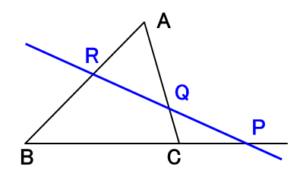
メネラウスの定理の導出
点 $A,B,C$ から直線 $\overline{PQR}$ に下した垂線の交点を $A’,B’,C’$ とします。
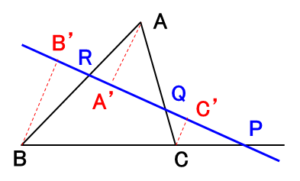
この場合、$AA’\parallel BB’\parallel CC’$ であるため、
$$\frac{BP}{PC}=\frac{BB’}{CC’}$$$$\frac{CQ}{QA}=\frac{CC’}{AA’}$$$$\frac{AR}{RB}=\frac{AA’}{BB’}$$
これらの両辺の積を取ると①が得られます。
$$\frac{BP}{PC}\cdot\frac{CQ}{QA}\cdot\frac{AR}{RB}=\frac{BB’}{CC’}\cdot\frac{CC’}{AA’}\cdot\frac{AA’}{BB’}=1$$
多角形の場合
メネラウスの定理は、四角形以上の多角形の場合での成り立ちます。ある直線が四角形 $A_1A_2A_3A_4$ の4辺 $A_1A_2,A_2A_3,A_3A_4,A_4A_1$ またはその延長とそれぞれ点 $P_1,P_2,P_3,P_4$ で交わるときに以下の関係が成り立ちます(②の導出)。
$$\frac{A_1P_1}{P_1A_2}\cdot\frac{A_2P_2}{P_2A_3}\cdot\frac{A_3P_3}{P_3A_4}\cdot\frac{A_4P_4}{P_4A_1}=1 -②$$
また、一般に $n$ 角形の場合は、メネラウスの定理は以下で表されます。
$$\frac{A_1P_1}{P_1A_2}\cdot\frac{A_2P_2}{P_2A_3}\cdots\frac{A_{n-1}P_{n-1}}{P_{n-1}A_n}\cdot\frac{A_nP_n}{P_nA_1}=1$$
②を導く
点 $A_1,A_2,A_3,A_4$ から直線 $\overline{P_1P_2P_3P_4}$ に下した垂線の交点を $A’_1,A’_2,A’_3,A’_4$ とします。
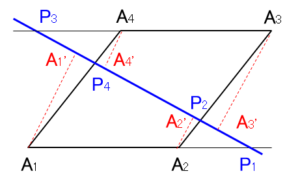
この場合、$A_1A’_1\parallel A_2A’_2\parallel A_3A’_3\parallel A_4A’_4$ であるため、
$$\frac{A_1P_1}{P_1A_2}=\frac{A_1A’_1}{A_2A’_2}$$$$\frac{A_2P_2}{P_2A_3}=\frac{A_2A’_2}{A_3A’_3}$$$$\frac{A_3P_3}{P_3A_4}=\frac{A_3A’_3}{A_4A’_4}$$$$\frac{A_4P_4}{P_4A_1}=\frac{A_4A’_4}{A_1A’_1}$$
これらの両辺の積を取ると②が得られます。
$$\frac{A_1P_1}{P_1A_2}\cdot\frac{A_2P_2}{P_2A_3}\cdot\frac{A_3P_3}{P_3A_4}\cdot\frac{A_4P_4}{P_4A_1}$$$$=\frac{A_1A’_1}{A_2A’_2}\cdot\frac{A_2A’_2}{A_3A’_3}\cdot\frac{A_3A’_3}{A_4A’_4}\cdot\frac{A_4A’_4}{A_1A’_1}=1$$




