ロルの定理
ロルの定理とは、関数 $f(x)$ が区間 $[a,b]$ で微分可能で $f(a)=f(b)$ ならば、
$$f'(c)=0$$
となる点 $C$ が区間 $[a,b]$ に存在することを示す定理です。言い換えると、
$$f’\big(a+\theta(b-a)\big)=0 (0\lt\theta\lt1) -①$$
となる $\theta$ が少なくとも1つ存在します。
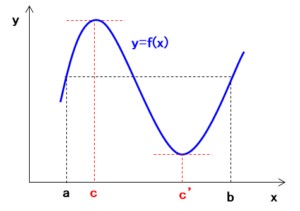
ロルの定理を導く
$f(x)$ は、区間 $[a,b]$ で微分可能なので連続関数になります。ある区間で定数でない連続関数は最大値と最小値を持ちます。最大値を $f(c)$ とすると、
$$f(c+h)-f(c)\le0 (\,|h|\lt c-a\,,\,|h|\lt b-c\,)$$
従って、
$$\frac{f(c+h)-f(c)}{h}\le0 (h\gt0)$$$$\frac{f(c+h)-f(c)}{h}\ge0 (h\lt0)$$
$f(x)$ は点 $c$ で微分可能であるため、$h\to0$ とすると、
$$f'(c)\le0$$$$f'(c)\ge0$$
であるため $f'(c)=0$ が得られます。
平均値の定理
平均値の定理とは、ロルの定理の前提条件を $f(a)\ne f(b)$ のように一般化した場合の定理で、関数 $f(x)$ が区間 $[a,b]$ で微分可能ならば、
$$f’\big(a+\theta(b-a)\big)=\frac{f(b)-f(a)}{b-a} (0\lt\theta\lt1) -②$$
となる $\theta$ が少なくとも1つ存在します。
平均値の定理を導く
2点 $\big(a,f(a)\big)$ 、$\big(b,f(b)\big)$ を結ぶ直線を考えると、その傾きは、
$$k=\frac{f(b)-f(a)}{b-a}$$
であるため、その方程式は以下になります。
$$f(x)-f(a)=k(x-a)$$
次の関数を定義すると、
$$F(x)\equiv f(x)-f(a)-k(x-a)$$
この関数は $F(a)=F(b)=0$ で、微分可能であるため、
$$F'(x)=f'(x)-k$$
ロルの定理より、区間 $[a,b]$ に以下のような $c$ が存在するため、②が導かれます。
$$F'(c)=f'(c)-k=f'(c)-\frac{f(b)-f(a)}{b-a}=0$$$$f'(c)=\frac{f(b)-f(a)}{b-a}$$




