初等関数の公式 - 理数の散策路

初等関数
微分公式

初等関数

指数関数

指数関数とは、以下のように冪における指数 $x$ を変数とする関数ですが、

$$y=a^x$$

狭義では、以下のネイピア数 $e$ を底とする指数関数を指します。

$$y=e^x$$$$e\equiv\lim_{n \to \infty}\Big(1+\frac{1}{n}\Big)^n\cong2.718$$

対数関数

対数関数 $\log$ の公式を指数との対比で整理します。

指数	対数
$a^x=y$	$x=\log_a{y}$
$a^0=1$	$0=\log_a{1}$
$a^1=a$	$1=\log_a{a}$
$a^x\cdot a^y = a^{x+y}$	$\log_a{xy}=\log_a{x}+\log_a{y}　-①$
$$\frac{a^x}{a^y}=a^{x-y}$$	$$\log_a{\frac{x}{y}}=\log_a{x}-\log_a{y}　-②$$
$a^y=x^b$（$a^{y/b}=x$）	$\log_a{x^b}=b\log_a{x}　-③$
$x=a^y$	$$\log_a{x}=\frac{\log_b{x}}{\log_b{a}}　-④$$

［③の導出］
$a^y=x^b$ の対数を取ると $y=\log_a{x^b}$ 、$a^{y/b}=x$ の対数を取ると $y/b=\log_a{x}$ より、$y$ を削除すると対数の公式が得られます。

［④の導出］
$x=a^y$ を $a$ と $b$ で対数を取ると $\log_a{x}=y$ 、$\log_b{x}=y\log_b{a}$ より、$y$ を削除すると対数の公式が得られます。

三角関数

三角関数は直角三角形の各辺の比として定義されます。

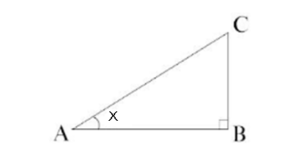
$$\sin{x}\equiv\frac{BC}{AC}$$$$\cos{x}\equiv\frac{AB}{AC}$$$$\tan{x}\equiv\frac{BC}{AB}=\frac{\sin{x}}{\cos{x}}$$

その他、三角関数には以下の関係式が成り立ちます。

$$\sin^2{x}+\cos^2{x}=1$$$$\sin{x}\lt x\lt\tan{x}　　(0\le x\le \pi/2)$$$$\lim_{x\to0}\frac{\sin x}{x}=1$$

三角関数の加法定理は以下になります。以下の式は⑥と⑦より導くことができます。

$$\sin{(x+y)}=\sin{x}\cos{y}+\cos{x}\sin{y}$$$$\cos{(x+y)}=\cos{x}\cos{y}-\sin{x}\sin{y}$$$$\sin{x}+\sin{y}=2\sin{\left(\frac{x+y}{2}\right)}\cos{\left(\frac{x-y}{2}\right)}$$$$\cos{x}+\cos{y}=2\cos{\left(\frac{x+y}{2}\right)}\cos{\left(\frac{x-y}{2}\right)}$$

双曲線関数

双曲線関数は以下で定義されます。

$$\cosh{x}\equiv\frac{e^x+e^{-x}}{2}　　-⑧$$$$\sinh{x}\equiv\frac{e^x-e^{-x}}{2}　　-⑨$$$$\tanh{x}\equiv\frac{\sinh{x}}{\cosh{x}}$$

双曲線関数には以下の関係式が成り立ちます。以下の式は⑧と⑨より導くことができます。

$$e^x=\cosh{x}+\sinh{x}$$$$\cosh^2{x}-\sinh^2{x}=1$$$$\sinh{x}=-i\sin{(ix)}$$$$\cosh{x}=\cos{(ix)}$$

双曲線関数の加法定理は以下になります。以下の式は⑧と⑨より導くことができます。

$$\sinh{(x+y)}=\sinh{x}\cosh{y}+\cosh{x}\sinh{y}$$$$\cosh{(x+y)}=\cosh{x}\cosh{y}+\sinh{x}\sinh{y}$$$$\sinh{x}+\sinh{y}=2\sinh{\Big(\frac{x+y}{2}\Big)}\cosh{\Big(\frac{x-y}{2}\Big)}$$$$\cosh{x}+\cosh{y}=2\cosh{\Big(\frac{x+y}{2}\Big)}\cosh{\Big(\frac{x-y}{2}\Big)}$$

オイラーの公式

オイラーの公式により、指数関数と三角関数が関係が示されます。

$$e^{ix}=\cos{x}+i\sin{x}　　-⑤$$

オイラーの公式より、以下の関係式は導かれます。

$$e^{2\pi i}=1$$$$e^{ix}=e^{i(x+2n\pi)}$$$$\cos{x}=\frac{e^{ix}+e^{-ix}}{2}　　-⑥$$$$\sin{x}=\frac{e^{ix}-e^{-ix}}{2i}　　-⑦$$

［⑤の導出］
関数 $f(x)=e^{-ix}(\cos x +i\sin x)$ を定義します。両辺の微分をとると $f'(x)=0$ より、$f(x)$ は一定値となります。これより、$f(x)=f(0)=1$ と置き、両辺に $e^{ix}$ を掛けると⑤が得られます。

微分公式

微分とは、関数などの値の変化率を測るものです。関数 $f(x)$ の微分は次のように定義されます。

$$\frac{dy(x)}{dx}=\lim_{h \to0}\frac{y(x+h)-y(x)}{h}$$

べき関数

べき関数の微分は以下になります。

$$\frac{d}{dx}(x^a)=ax^{a-1}$$

導出

べき関数の微分は定義から求めることができます。$(x+h)^a$ をテイラー展開して、$h\to0$ としています。

$$\frac{d}{dx}(x^a)=\lim_{h\to0}\frac{(x+h)^a-x^a}{h}$$$$=
\lim_{h\to0}\frac{1}{h}\left[x^a\Big(1+\frac{ah}{x}+\frac{a(a-1)h^2}{x^2}+\cdots\Big)-x^a\right]=ax^{a-1}$$

指数関数

指数関数の微分は以下になります。

$$\frac{d}{dx}(a^x)=a^x \ln{a}$$$$\frac{d}{dx}(e^x)=e^x$$

導出

$a^h-1=1/t$（$h\to0$ で $t\to\infty$）と置くと、

$$h=\log_a\Big(1+\frac{1}{t}\Big)$$

微分の定義より、

$$\frac{d}{dx}(a^x)=a^x\lim_{h\to 0}\frac{a^h-1}{h}$$$$=
a^x\lim_{t\to\infty}\frac{1}{t\log_a\Big(1+\frac{1}{t}\Big)}=a^x\frac{1}{\log_ae}=a^x\ln{a}$$

途中、次のネイピア数の定義を使っています。

$$\lim_{t\to\infty}\Big(1+\frac{1}{t}\Big)^t=e$$

対数関数

対数関数の微分は以下になります。

$$\frac{d}{dx}\left(\log_ax\right)=\frac{1}{x\ln{a}}$$$$\frac{d}{dx}\left(\ln{x}\right)=\frac{1}{x}$$

導出

$\log_a{x}=y$ と置くと、$x=a^y$ であるから、両辺を $x$ で微分すると、

$$1=\frac{dy}{dx}a^y\ln{a}=\frac{dy}{dx}x\ln{a}$$

自然対数の場合は、$a=e$ と置くと得られます。

三角関数

三角関数の微分は以下になります。

$$\frac{d}{dx}(\sin{x})=\cos{x}$$$$\frac{d}{dx}(\cos{x})=-\sin{x}$$$$\frac{d}{dx}(\tan{x})=\frac{1}{\cos^2{x}}$$

導出

微分の定義式より、

$$\frac{d}{dx}(\sin{x})=\lim_{h\to0}\frac{\sin(x+h)-\sin x}{h}$$$$=
\lim_{h\to0}\frac{2\cos{\left(x+\frac{h}{2}\right)}\sin{\left(\frac{h}{2}\right)}}{h}=\cos{x}$$

$$\frac{d}{dx}(\cos{x})=\lim_{h\to0}\frac{\cos(x+h)-\cos x}{h}$$$$=
\lim_{h\to0}\frac{-2\sin{\left(x+\frac{h}{2}\right)}\sin{\left(\frac{h}{2}\right)}}{h}=-\sin{x}$$

ここで、次の近似を使っています。

$$\lim_{h\to0}\Big(\sin{\frac{h}{2}}\Big)=\frac{h}{2}$$

尚、$\tan$ については以下の計算より得られます。

$$\frac{d}{dx}(\tan{x})=\frac{d}{dx}\Big(\frac{\sin{x}}{\cos{x}}\Big)$$