ニューラルネットワークとは

ニューラルネットワーク
ネットワーク関数
誤差の評価
誤差逆伝播法

ニューラルネットワーク

ニューラルネットワークとは、脳機能の特性に類似した数理的モデルです。ニューロン（神経細胞）とシナプス（ニューロンの接合部分）からネットワークを形成し、学習によってシナプスの結合強度を変化させ、問題解決を行います。

ネットワーク関数

ニューロンを配置する層は、入力層、中間層、出力層などに分かれています。以下は、中間層が１層の場合のモデルを取り上げます。

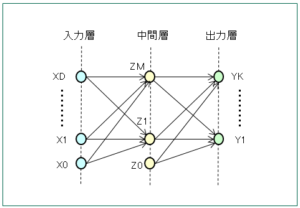
まず、入力層（ $x_{0}, x_{1}, \dots, x_{D}$ ）から中間層（ $z_{0}, z_{1}, \dots, z_{M}$ ）への伝播は以下の線形和で表します。

$a_{j} = \sum_{i = 0}^{D} w_{j i}^{(1)} x_{i}, x_{0} = 1 － ①$

$z_{j} = h (a_{j})$

ここで、 $w_{j i}^{(1)}$ は重みパラメタ、 $w_{j 0}^{(1)}$ はバイアスパラメタです。 $a_{j}$ は活性と呼ばれ、活性化関数 $h$ で変換され中間層に渡されます。活性化関数には、 $\tanh$ 関数や以下のロジスティックシグモイド関数などが使われます。

$h (a_{j}) = \frac{1}{1 + e^{- a_{j}}}$

次に、中間層から出力層（ $y_{0}, y_{1}, \dots, y_{K}$ ）への伝播は以下の線形和で表します。活性化関数 $σ$ にはロジスティックシグモイド関数などが使われます。

$a_{k} = \sum_{j = 0}^{M} w_{k j}^{(2)} z_{j}, z_{0} = 1 － ②$

$y_{k} = σ (a_{k})$

①と②の合わせると、入力層から出力層への伝播は以下でまとめられます。

$y_{k} (x, w) = σ (\sum_{j = 0}^{M} w_{k j}^{(2)} h (\sum_{i = 0}^{D} w_{j i}^{(1)} x_{i}))$

誤差の評価

誤差の評価により、ニューラルネットワークの重みパラメタ $w$ を求めます。具体的には、入力ベクトル $x_{n}$ の集合に対する目標ベクトル $t_{n}$ が与えられたとき、次の二乗和誤差を最小にする重みパラメタを求めることです。

$E (w) = \frac{1}{2} \sum_{n = 1}^{N} | y (x_{n}, w) - t_{n} |^{2}$

この二乗和誤差を最小（極小）にするための条件は以下で表されます。

$\nabla E (w) = \sum \frac{\partial E}{\partial w_{i j}} = 0 － ③$ $\frac{\partial^{2} E}{\partial w_{i j}^{2}} > 0$

誤差逆伝播法

誤差逆伝搬法（Backpropagation Method）とは、ニューラルネットワークを学習させる際に用いられるアルゴリズムです。中間層について、次のようなモデルを想定います。

$z_{j} = h (a_{j}), a_{j} = \sum_{i} w_{j i}^{(1)} x_{i} － ④$ $y_{k} = h (a_{k}), a_{k} = \sum_{j} w_{k j}^{(2)} z_{j} － ⑤$

ここで、誤差 $δ$ を以下で定義します。

$δ_{j} \equiv \frac{\partial E}{\partial a_{j}} － ⑥$

$δ_{k} \equiv \frac{\partial E}{\partial a_{k}} ≅ y_{k} - t_{k} － ⑦$

誤差逆伝搬法の手順

誤差逆伝搬法の手順は以下になります。

④と⑤より、順伝播で全ての中間層と出力層の値を求める。
⑦より、出力層の誤差 $δ_{k}$ を計算する。
⑧より、誤差 $δ$ を逆伝搬させ、全ての中間層の誤差を求める。
$δ_{j} = \sum_{k} δ_{k} w_{k j}^{(2)} h^{'} (a_{j}) － ⑧$
⑨と⑩より、極小条件③を評価する。
$\frac{\partial E}{\partial w_{j i}^{(1)}} = δ_{j} x_{i} － ⑨$ $\frac{\partial E}{\partial w_{k j}^{(2)}} = δ_{k} z_{j} － ⑩$

⑧の導出

まず、⑥と⑦より、

$δ_{j} = \sum_{k} \frac{\partial E}{\partial a_{k}} \frac{\partial a_{k}}{\partial a_{j}} = \sum_{k} δ_{k} \frac{\partial a_{k}}{\partial a_{j}} － (1)$