フェルミ・ディラック統計
フェルミ・ディラック統計とは、相互作用のないフェルミ粒子(フェルミオン)が従う量子統計で、あるエネルギー準位の粒子数の分布を与えます。フェルミ粒子とは、系の波動関数が任意の2粒子の交換に対して符号を変える(反対称)粒子です。
量子力学においては、局所化された2つの同種の粒子は区別することができないため、同種の多粒子系の波動関数については、フェルミ・ディラック統計とボーズ・アインシュタイン統計のみがシュレディンガー方程式の解として許されています。
フェルミ分布関数
フェルミ分布関数 $f$ は、エネルギー準位を $\epsilon_k$、化学ポテンシャルを $\mu$、温度を $T$、ボルツマン定数を $k$ とすると以下で表されます。尚、$n_k$ は1つのエネルギー準位の粒子数の平均、$N$ は全粒子数です。
$$f(\epsilon_k)=\frac{\bar{n}_k}{N}=\frac{1}{e^{(\epsilon_k-\mu)/kT}+1}$$
フェルミ分布関数は $0\sim1$ の間の値をとります。また、$\epsilon_k=\mu$ で $f(\mu)=1/2$ となることが分かります。
高エネルギーの場合
$\epsilon_k\gg1$ で $e^{(\epsilon_k-\mu)/kT}\gg1$ となるため、
$$f(\epsilon)\propto e^{-\epsilon/kT}$$
高エネルギーの場合は、マックスウェル分布に近似されることが分かります。
低エネルギーの場合
$\epsilon_k\lt\mu$ の場合は指数の中は負になるため、温度を0に近づけると、$e^{(\epsilon_k-\mu)/kT}\to0$ となり、フェルミ分布関数は1になります。
$$f(\epsilon_k)=\lim_{T\to0}\frac{1}{e^{(\epsilon_k-\mu)/kT}+1}=1$$
$\epsilon_k\gt\mu$ の場合は指数の中は正になるため、温度を0に近づけると、$e^{(\epsilon_k-\mu)/kT}\to\infty$ となり、フェルミ分布関数は0になります。
$$f(\epsilon_k)=\lim_{T\to0}\frac{1}{e^{(\epsilon_k-\mu)/kT}+1}=0$$
尚、このときの $\mu$ はフェルミエネルギー $\epsilon_F$ と呼ばれています。
フェルミ分布関数の導出
量子状態のエネルギー準位を低い方から $g_k$ づつのグループに分け、それに粒子数 $n_k$ を割当てるとします。尚、フェルミ粒子の場合、パウリの排他律により、量子状態を占める粒子の数は1か0であるため、
$$g_k\gt n_k$$
これは、$g_k$ 個の箱に $n_k$ のボールを入れる問題で、1つの箱に入れるボールの数は1個までとなります。
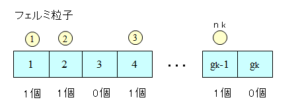
この場合の1つのグループ当りの状態(組合せ)の数は、
$$\frac{g_k!}{n_k!(g_k-n_k)!}$$
全てのグループの状態の数 $G$ は、これの積になるため、
$$G=\prod_k\frac{g_k!}{n_k!(g_k-n_k)!} -①$$
尚、以下の全粒子数 $N$ と全エネルギー $E$ は一定と考えます。
$$\sum_kn_k=N -②$$$$\sum_k\epsilon_kn_k=E -③$$
実際に起こりうるのは最も状態数が多い場合、つまり $G$ が停留値をもつ場合です。まず、①の対数をとり、スターリンの公式
$$\ln{n!}\cong n\ln{n}-n$$
を使うと、
$$\ln{G}=\sum_k\Big(g_k\ln{g_k}-n_k\ln{n_k}-(g_k-n_k)\ln{(g_k-n_k)}\Big)$$
これに変分 $\delta$ をとり、$\delta g_k=0$ であるから、停留値の条件は以下になります。
$$\delta\ln{G}=\sum_k\Big(-\ln{n_k}+\ln{(g_k-n_k)}\Big)\delta n_k=0 -①’$$
②と③についても停留値の条件は、
$$\sum_k\delta n_k=0 -②’$$$$\sum_k\epsilon_k\delta n_k=0 -③’$$
②’と③’の条件の下、①’を満たす条件を求めるため、ラグランジュ乗数法を用います。ここで、$\alpha$ と $\beta$ は定数です。
$$\sum_k\Big(\ln{\frac{n_k}{g_k-n_k}}+\alpha+\beta\epsilon_k\Big)\delta n_k=0$$
この括弧の中が0になるための条件は以下になります。
$$n_k=\frac{g_ke^{-\alpha-\beta\epsilon_k}}{1+e^{-\alpha-\beta\epsilon_k}}=\frac{g_k}{e^{\alpha+\beta\epsilon_k}+1}$$
各グループでの平均を取ると、
$$\bar{n}_k=\frac{n_k}{g_k}=\frac{1}{e^{\alpha+\beta\epsilon_k}+1}$$
古典統計からの類推で $\beta=1/kT$ と置き、条件②を満たすように $\alpha$ を定めると、以下の関係式が得られます。
$$\bar{n}_k\propto\frac{1}{e^{\epsilon_k/kT}+1}$$




