命題論理とは、命題をいくつかの記号(論理記号)に置換えて単純化して表現したものです。尚、命題とは、真偽の判断の対象となる文章(論理式)です。
論理記号
以下に、命題論理で使われる論理記号について説明します。
含意($\to$)
命題 $A$、$B$ について、「$A$ であれば $B$ である」ことを以下のように表します。言い換えれば、$A$ であることが証明できれば、$B$ であることも証明できるという意味になります。
$$A\to B$$
定義より、次のことが分かります。
$$A\to A$$
否定($\neg$)
命題 $A$ について、「$A$ でない」ことを以下のように表します。
$$\neg A$$
定義より、次のことが分かります。
$$\neg\neg A\to A$$$$A\to\neg\neg A$$
同値($\equiv$)
2つの論理式 $A\to B$ と $B\to A$ が両方証明できることを「同値である」といい、以下のように表します。これは、「$A$ ならば $B$ であり、かつ、$B$ ならば $A$ である」と同じ意味であると考えます。
$$A\equiv B$$
定義より、次のことが分かります。
$A\equiv B$ 、$B\equiv C$ ならば、$A\equiv C$
$\neg\neg A\equiv A$
論理和($\vee$)
命題 $A$、$B$ について、「$A$ または $B$」であることを以下のように表します。
$$A\vee B$$
また、この論理和は次のように表すことができます。
$$A\vee B\equiv\neg A\to B$$
論理積($\wedge$)
命題 $A$、$B$ について、「$A$ かつ $B$」であることを以下のように表します。
$$A\wedge B$$
また、この論理和は次のように表すことができます。
$$A\wedge B\equiv\neg(\neg A\vee\neg B)$$
公理と公式
ヒルベルトの公理系
命題論理における、ヒルベルトの公理系は以下で表されます。
- $A\to(B\to A)$
- $[A\to(B\to C)]\to[(A\to B)\to(A\to C)]$
- $(\neg B\to\neg A)\to(A\to B)$
これらの公理を単純化して図に表すと以下になります。
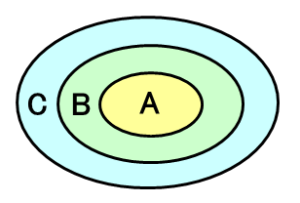
- $A$ が成り立つならば、$B$ が成り立つ場合も、$A$ は成り立つ。
($A$ が成り立つならば、どのような仮定を置いても $A$ は成り立つ) - $A$ が成り立つ前提で、$B$ が成り立つ場合に $C$ が成り立てば、これを前提に、
$A$ が成り立つ場合に $B$ が成り立てば、$A$ が成り立つ場合に $C$ が成り立つ。 - $B$ が成り立たない場合に $A$ が成り立たなければ、$A$ が成り立つ場合に $B$ が成り立つ。
推論規則
推論規則として以下を仮定します。
- $(A\wedge(A\to B))\to B$
- $((A\to B)\wedge(B\to C))\to(A\to C)$
これらを言葉で表すと以下になります。
- $A$ が成り立ち、かつ、$A$ が成り立つ場合に $B$ が成り立てば、$B$ が成り立つ。
- $A$ が成り立つ場合に $B$ が成り立ち、かつ、$B$ が成り立つ場合に $C$ が成り立つならば、$A$ が成り立つ場合に $C$ が成り立つ。
背理法
背理法とは、ある仮定が矛盾することを示すことで、その仮定が成り立たないことを証明する手法です。元の仮定{$C_1,\cdots,C_n$}に $C_{n+1}$ を追加して、仮定{$C_1,\cdots,C_n,C_{n+1}$}が矛盾すれば、元の仮定に対し $\neg C_{n+1}$ が証明できたことになります。
尚、矛盾とは、ある仮定の下で、論理式 $A$ とその否定 $\neg A$ の両方が証明できてしまうことを言います。
ド・モルガンの法則
ド・モルガンの法則は以下のように表されます。
$$\neg(A\vee B)\equiv\neg A\wedge\neg B$$$$\neg(A\wedge B)\equiv\neg A\vee\neg B$$




