シャノンの通信路定理とは

シャノンの定理とは

シャノンの定理とは、誤りの生じる（雑音のある）通話路であっても、誤りのない情報の伝送速度を、通話路容量に近づけられることを示した定理です。

通話路の容量を $C$ 、情報伝達速度を $R$ とすると、任意に小さい誤り確率 $ϵ$ で送れる符号化が存在することを示しています。

$R = C - ϵ (ϵ > 0)$

通信路の入力側につながれた情報源の１秒当たりのエントロピーを $H (X)$ 、送信信号の不確定度を表すエントロピーを $H_{Y} (X)$ とした場合、情報伝達速度 $R$ は以下で表されます。尚、 $H_{Y} (X)$ は情報の「あいまい度」と呼ばれています。

$R = H (X) - H_{Y} (X) - ①$

文字の種類が $k$ の場合のエントロピー（文字を表現するためのビット数）は、

$H = \log_{2} k$

文字数が $N$ の文字系列の総数は以下になります。

$k^{N} = 2^{H N}$

従って①より、送信信号（入力）の文字列の総数は $2^{H (X) N}$ となります。この中から確実に送信できるのは、情報伝達速度分である $2^{R N}$ と考えることができるため、その確率は、

$\frac{2^{R N}}{2^{H (X) N}} = 2^{[R - H (X)] N} = 2^{- H_{Y} (X) N} - ②$

その逆の確実に送信できない確率は以下で表されます。

$1 - 2^{- H_{Y} (X) N} - ③$

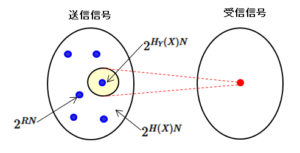
１つの受信信号（下図赤点）に対する送信信号（文字数列）の候補の数は、情報のあいまい度 $H_{Y} (X)$ により $2^{H_{Y} (X) N}$ （下図黄色）となります。尚、送信信号の総数は $2^{H (X) N}$ で、確実に送信できる数は $2^{R N}$ （下図青点）です。

この $2^{H_{Y} (X) N}$ （黄色）の中に１つだけ②の確率で現れる文字数列（青点）があればよいので、それ以外の文字数列（ $2^{H_{Y} (X) N} - 1$ ）が確実に送信できない文字数列であるための確率 $P$ は、③により以下で表されます。

$P = (1 - 2^{- H_{Y} (X) N})^{2^{H_{Y} (X) N} - 1}$

この確率 $P$ は、２つの異なる送信信号に対して、同じ受信信号が発生してしまう確率になります。ここで、十分に長い文字数列（ $N ≫ 1$ ）を仮定とすると、 $2^{- H_{Y} (X) N} ≪ 1$ より、テイラー展開することができて、

$P ≅ 1 - 2^{- H_{Y} (X) N} (2^{H_{Y} (X) N} - 1) ≅ 0$

これにより文字数列を長く取ることにより、１つの送信信号に対し１つの受信信号を対応させることができる、つまり雑音による影響を限りなく小さくできることが分かります。