アンペールの法則
アンペールの法則とは、電流とその周りにできる磁場との関係を表した法則です。19世紀前半にアンペールによって発見されました。
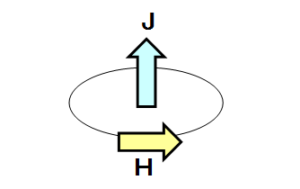
任意の閉回路にそって磁場の大きさ $H$ を足し合わせると、閉回路を貫く電流の和 $J$ に比例します。式で表すと以下になります。
$$2\pi rH=J$$
これを積分形式で表すと以下になります。尚、左辺の積分は、閉回路の周回積分を表します。
$$\oint{\bf H}\cdot d{\bf s}=J$$
この左辺をストークスの定理を用いて面積分に書き直し、右辺を電流密度 $j$ を使って書き直すと、
$$\int_S\nabla\times{\bf H}\cdot d{\bf S}=\int_S{\bf j}\cdot d{\bf S}$$
となるため、以下の式が得られます。
$$\nabla\times{\bf H}={\bf j} -①$$
これが、微分形式で表されたアンペールの法則で、マクスウェル方程式の1つに含まれています。尚、磁場 $H$ と電流 $J$ の向きは右ネジの関係になります。
変位電流
変位電流とは、電束密度 $D$ の時間的な変位によって発生する電流です。通常の電流は電荷の移動で発生しますが、変位電流は電荷の移動で発生するものではないため「変位」と呼ばれています。
$$J_D=\frac{d}{dt}\int_S{\bf D}\cdot d{\bf S}$$
例えば、コンデンサを流れる電流の場合は、実際には電極間の電荷の移動はありませんが、電極間の電場の時間的な変位に比例した電流が流れたと考えることができます。
この変位電流を考慮して①を書き換えると、一般化されたアンペールの法則が導かれます。
$$\nabla\times{\bf H}={\bf j}+\frac{\partial{\bf D}}{\partial t}$$
ビオ・サバールの法則
ビオ・サバールの法則とは、電流の存在によってその周りに生じる磁場を計算するための法則です。この法則は、静電場でのクーロンの法則に対応します。
$${\bf H}=\frac{1}{4\pi}\frac{q}{r^2}\frac{{\bf v}\times{\bf r}}{r}=\frac{1}{4\pi}\int\frac{{\bf j}\times{\bf r}}{r^3}dV$$
この式からも、磁場と電流の方向が右ネジの法則であることが分かります。
単位まとめ
| 名称 | 記号 | 単位 | 次元 |
| 電流密度 | $j$ | $A/m^2$ | $L^{-2}I$ |
| 電場の強さ | $E$ | $V/m$ | $MLT^{-3}I^{-1}$ |
| 磁場の強さ | $H$ | $A/m$ | $L^{-1}I$ |
| 電束密度 | $D$ | $C/m^2$ | $L^{-2}TI$ |
| 磁束密度 | $B$ | $T$(テスラ) | $MT^{-2}I^{-1}$ |




