ホイヘンスの原理
ホイヘンスの原理とは、光を波動論的に説明した理論です。波の媒体を力学的な模型として考えて、玉突きの球が一様に分布している空間を仮定し、衝突を繰り返すことで波が伝搬していくと考えました。
その後、フレネルは波動論の観点から整理し、光の波動説を確立しました。このため、ホイヘンス・フレネルの原理と呼ばれることもあります。
フレネルの考え方によると、ある時刻の波面上 $\overline{AB}$ の各点が入射波により揺さぶられて、周りの空間に球面波(素元波または2次波)を作り出し、それらの球面波の包絡線が我々に観測されると考えます。尚、素元波自体は観測されません。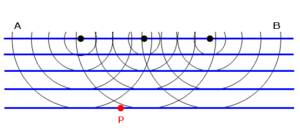
点 $P$ における変位は、波面上 $\overline{AB}$ の各点から作り出される素元波の和で表されます。
$$\phi_P=\sum_{\overline{AB}}\Delta\phi_i$$
これを具体的に計算する方法はキルヒホッフにより求められました(キルヒホッフの積分表示)。
キルヒホッフの積分表示
キルヒホッフの積分表示とは、波の伝搬について、ホイヘンスの原理を数学的に定式化したものです。以下の波動方程式を満たすポテンシャルを $\phi$ について、
$$\nabla^2\phi+k^2\phi=0 -①$$
点 $r_0$ での $\phi$ の値を、$r_0$ を囲む閉曲面 $S$ 上の点の $\phi$ の値を用いて、以下のように表すことができます。
$$\phi(r_0)=\frac{1}{4\pi}\int\Big(\frac{e^{ikr}}{r}\nabla\phi-\phi\nabla\frac{e^{ikr}}{r}\Big)\cdot{\bf n}dS -②$$
キルヒホッフの積分表示を導く
ベクトル公式、
$$\nabla\cdot(\psi{\bf A})={\bf A}\cdot\nabla\psi+\psi\nabla\cdot{\bf A}$$
を利用して ${\bf A}\to\nabla\phi$ と置くと、
$$\nabla\cdot(\psi\nabla\phi)=\nabla\phi\cdot\nabla\psi+\psi\nabla^2\phi$$
この式から、この式の $\phi$ と $\psi$ を入れ替えた式を差し引くと、以下が得られます。
$$\nabla\cdot(\psi\nabla\phi-\phi\nabla\psi)=\psi\nabla^2\phi-\phi\nabla^2\psi$$
この両辺の体積分を行い、ガウスの定理を使うと、
$$\int(\psi\nabla^2\phi-\phi\nabla^2\psi)dV=\int\nabla\cdot(\psi\nabla\phi-\phi\nabla\psi)dV$$$$=\int(\psi\nabla\phi-\phi\nabla\psi)\cdot{\bf n}dS -③$$
ここで $\psi$ をヘルムホルツ方程式の解とし、
$$(\nabla^2+k^2)\psi=-4\pi\delta({\bf r}) -④$$$$\psi=\frac{e^{ikr}}{r}$$
①と④を③に代入すると②が得られます。
$$4\pi\int\phi\delta({\bf r})dV=\int\Big(\frac{e^{ikr}}{r}\nabla\phi-\phi\nabla\frac{e^{ikr}}{r}\Big)\cdot{\bf n}dS$$




