純粋戦略でのナッシュ均衡
ナッシュ均衡とは、他の人々が戦略を変えない限り、自分の戦略を変える動機(メリット)を持たない状態です。まず、純粋戦略の場合のナッシュ均衡について説明します。
純粋戦略とは、各プレイヤが1つの戦略のみ選択できる場合です。以下は簡単のため、プレイヤが2人、戦略が2つ(戦略 $X$ ,戦略 $Y$ )の場合で考えます。以下の利得行列では、各プレイヤの戦略と利得の関係を表しています。
例えば、プレイヤ1が戦略 $X$ 、プレイヤ2が戦略 $Y$ を取る場合の戦略の組 $(X,Y)$ について、プレイヤ1の利得を $u_1^{XY}$、プレイヤ2の利得を $u_2^{XY}$ で表します。
| $1\backslash 2$ | $2:X$ | $2:Y$ |
| $1:X$ | $u_1^{XX}$ 、$u_2^{XX}$ | $u_1^{XY}$ 、$u_2^{XY}$ |
| $1:Y$ | $u_1^{YX}$ 、$u_2^{YX}$ | $u_1^{YY}$ 、$u_2^{YY}$ |
ナッシュ均衡とは、お互いの取る戦略がそれぞれ相手の戦略に対する最適反応戦略となっている場合です。例えば、戦略の組 $(X,X)$ がナッシュ均衡であるとは、以下の条件が成り立っている場合です。このとき、お互い自ら戦略を変えるメリットはないため、安定した組合せになります。
$$u_1^{XX}\ge u_1^{YX} , u_2^{XX}\ge u_2^{XY}$$
狭義ナッシュ均衡とは、お互いの取る戦略がそれぞれ相手の戦略に対する唯一の最適反応戦略となっているナッシュ均衡です。例えば、戦略の組 $(X,X)$ が狭義ナッシュ均衡であるとは、以下の条件が成り立っている場合です。
$$u_1^{XX}\gt u_1^{YX} , u_2^{XX}\gt u_2^{XY}$$
最適反応戦略
最適反応戦略とは、相手のある戦略のもとで、自分の利得を最大にする戦略です。例えば、以下の場合、プレイヤ2の戦略 $X$ に対するプレイヤ1の戦略 $X$ は最適反応戦略であると言います。
$$u_1^{XX}\ge u_1^{YX}$$
合理的なプレイヤであれば、常に最適反応戦略を選択すると考えます。
支配戦略
支配戦略とは、相手のどの戦略に対しても、自分の利得が大きくなる戦略です。例えば、プレイヤ1の場合、戦略 $X$ が支配戦略であるためには、以下の2つの条件が成り立つ必要があります。
$$u_1^{XX}\gt u_1^{YX} , u_1^{XY}\gt u_1^{YY}$$
弱支配戦略とは、相手のどの戦略に対しても、自分の利得が大きいか等しく、かつ、全ての条件が等しくならない戦略です。例えば、プレイヤ1の場合、戦略 $X$ が弱支配戦力であるためには、以下の2つの条件が成り立つ必要があります。
$$u_1^{XX}\ge u_1^{YX} , u_1^{XY}\ge u_1^{YY}$$
純粋戦略の例
純粋戦略の例をいくつか挙げます。
価格競争
一方が価格を維持している状態でもう一方が値引きすると、値引きした方の利益は大きくなりますが、両方が値引きすると、両者が価格を維持したときよりも利益は下がるケースです。
| 1$\backslash$2 | 2:維持 | 2:値引 |
| 1:維持 | 3 、3 | 1 、5 |
| 1:値引 | 5 、1 | 2 、2 |
この場合のナッシュ均衡は(値引、値引)の組み合わせになります。また、(値引、値引)は両者の支配戦略となっています。
規格の採用
両方がそれぞれ自社の規格を有しており、両方が同じ規格を採用した場合は、自社の規格を採用した方の利益が多くなりますが、両方が違う規格を採用した場合は、利益が最低となるケースです。
| 1$\backslash$2 | 2:1の規格を採用 | 2:2の規格を採用 |
| 1:1の規格を採用 | 5 、3 | 1 、1 |
| 1:2の規格を採用 | 1 、1 | 3 、5 |
この場合のナッシュ均衡は(規格1、規格1)と(規格2、規格2)の2つの組み合わせになります。尚、これらは両者の支配戦略とはなっていないケースです。
視聴率争い
双方が放送する番組により、以下のように視聴率が変わるケースです。
| 1$\backslash$2 | 2:映画 | 2:音楽 |
| 1:映画 | 5 、1 | 2 、4 |
| 1:音楽 | 3 、3 | 4 、2 |
この場合はナッシュ均衡は存在しません。また、支配戦略も存在しません。
混合戦略でのナッシュ均衡
混合戦略とは、各プレイヤが複数の戦略の組合せを選択できる場合を言います。純粋戦略の場合はナッシュ均衡が存在しないケースがありますが、混合戦略の場合は常にナッシュ均衡が存在することが以下のように示されます。
プレイヤ1が戦略 $X$ をとる割合を $p$($0\le p\le1$)、プレイヤ2が戦略 $X$ をとる割合を $q$($0\le q\le1$)とすると、利得行列の各戦略の組が起こりうる割合は以下になります。
| $A\backslash B$ | $2:X$ | $2:Y$ |
| $1:X$ | $pq$ | $p(1-q)$ |
| $1:Y$ | $(1-p)q$ | $(1-p)(1-q)$ |
プレイヤ1の最適反応戦略
プレイヤ1の利得を計算します。
$$u_1=pqu_1^{XX}+p(1-q)u_1^{XY}+(1-p)qu_1^{YX}+(1-p)(1-q)u_1^{YY}$$
これは、$\alpha,\beta,\gamma,\delta$ を定数とすると、以下にのように整理することができます。
$$u_1=(\alpha q-\beta)p+\gamma q+\delta$$
ここで、$p$ の係数($\alpha q-\beta$)に注目すると、これが正の場合は $p$ が大きいほど($p=1$)、負の場合は $p$ が小さいほど($p=0$)プレイヤ1の利得は大きくなります。この分岐点は、$q$ が以下の値の時です。
$$q=\frac{\beta}{\alpha}\equiv q_c$$
$\alpha$ が正のときは $q\gt q_c$、負のときは $q\lt q_c$ の場合に $p$ の係数は正になるため、プレイヤ1は $p=1$(戦略 $X$ のみ選択)とすることで利得を最大にできます。そうでない場合は、$p=0$(戦略 $Y$ のみ選択)となります。
これをグラフで表すと以下になります。プレイヤ1の最適反応戦略($q\gt q_c$ で $p=1$ の場合)は青線で表されます。
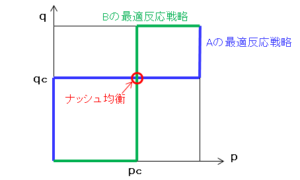
プレイヤ2の最適反応戦略
プレイヤ2でも同様の式が成り立つため、プレイヤ2の利得は、
$$u_2=pqu_2^{XX}+p(1-q)u_2^{XY}+(1-p)qu_2^{YX}+(1-p)(1-q)u_2^{YY}$$$$=(\alpha’ p-\beta’)q+\gamma’ p+\delta’$$
分岐点は以下になり、
$$p=\frac{\beta’}{\alpha’}\equiv p_c$$
$\alpha’$ が正のときは $p\gt p_c$、負のときは $p\lt p_c$ の場合に $q$ の係数は正になるため、プレイヤ2は $q=1$(戦略 $X$ のみ選択)とすることで利得を最大にできます。そうでない場合は、$q=0$(戦略 $Y$ のみ選択)となります。
従って、プレイヤ2の最適反応戦略($p\gt p_c$ で $q=1$ の場合)は上図の緑線で表されます。このときナッシュ均衡は、両者の最適反応戦略の交点で示されます。




